1. Алгебра
  2. Корень из х2+8х-9 корень

Корень из х2+8х-9 < корень из 11

Walker95 Walker95    3   06.03.2019 19:50    2

Ответы
1232960 1232960  24.05.2020 02:38

Область допустимых значений: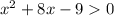 x^{2}+8x-90

\left \{ {{x9} \atop {x<1}} \right.

Решим неравенство методом интервалов:

\sqrt{x^{2}+8x-9}=\sqrt{11}

Возведем обе части уравнения в квадрат:

x^{2}+8x-9=11

x^{2}+8x-20=0

решаем по теореме Виета:

x1+ x2= -8

x1*x2=-20

x1=-10

x2=2

тогда -10<x<2

учитывая Область допустимых значений, ответ: -10<x<1

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
dashhach dashhach  15.11.2019 18:07
11*3(в 6 степени)* √11*2²= √2⁴*3²*5⁴= √2(в 6 степени) *3⁴*5²=...
kupecki kupecki  15.11.2019 18:03
Знайти область визначення функції y= [tex]\frac{1}{log_{\frac{1}{3} }x+1 }[/tex]...
19283746521 19283746521  15.11.2019 18:01
Ушбурыштын улкен бурышына карсы улкен кабыргасы,ал улкен кабыргасына карсы улкен бурышы жататынын далелдендер​...
Лилия22111048483 Лилия22111048483  15.11.2019 18:01
Решите уравнение с дробями! 2х+7 15 5х-8—— + = х-1 х^2-1 х-1...
SharagaXD SharagaXD  15.11.2019 18:01
Найдите сумму 2-5+8-11+14-17+-497+500...
aliyevasevgi5 aliyevasevgi5  15.11.2019 18:00
Освободитесь от иррациональности в знаменателе дроби 1/√7-√5...
Phelper Phelper  15.11.2019 18:00
Нужно найти значение выражения ​...
geralis728p0bgjl geralis728p0bgjl  15.11.2019 17:59
Найдите sin t, cjs t и th t, если a)t=0; б)t=п\2; в)t=3п\2; г)t=п...
alexnatur alexnatur  15.11.2019 17:57
Можете объяснить, как это делается. не просто тупо решить. ​...
kthjxrfqqq kthjxrfqqq  14.06.2019 16:20
1/4х-у=-5 1/2х-1/7у=3 решить систему неравенств...

Популярные вопросы