Координаты точки M (x; y) удовлетворяют равенству 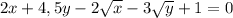$2x + 4,5y - 2 \sqrt{x} - 3 \sqrt{y} +1 =0$ . Найдите tg α, где α - угол, образуемый вектором OM с положительным направлением оси OX.

Координаты точки M (x; y) удовлетворяют равенству . Найдите tg α, где α - угол, образуемый вектором

Ответы

софа336 07.07.2021 23:15

4/9

Объяснение:

Координаты точки M (x; y) удовлетворяют равенству . Найдите tg α, где α - угол, образуемый вектором

ПОКАЗАТЬ ОТВЕТЫ

КаРаТиСтКиОкУшИнА 07.07.2021 23:15

ответ: 4/9

Объяснение:

Из прямоугольного треугольника (рисунок):

$tg\;\alpha=\dfrac{y}{x}$

Следовательно, необходимо найти частное y/x.

$2x+4,5y -2\sqrt x-3\sqrt y+1=0$

Соберём полные квадраты, добавив необходимое слагаемое. Для удобства можно провести замену u = √x, v = √y

$2x+4,5y -2\sqrt x-3\sqrt y+1=0\\ \\ (2x-2\sqrt x+\dfrac{1}{2})-\dfrac{1}{2}+(4,5y-3\sqrt y+\dfrac{1}{2})-\dfrac{1}{2}+1=0\\ \\ (\sqrt{2x} -\dfrac{1}{\sqrt 2})^2+(\dfrac{3\sqrt y}{\sqrt 2}-\dfrac{1}{\sqrt 2})^2=0$

Сумма квадратов равна нулю, когда каждое слагаемое равно нулю:

$(\sqrt{2x} -\dfrac{1}{\sqrt 2})^2=0\quad\quad\quad\quad(\dfrac{3\sqrt y}{\sqrt 2}-\dfrac{1}{\sqrt 2})^2=0\\ \\ \sqrt{2x} -\dfrac{1}{\sqrt 2}=0 \quad\; \quad\quad\quad\quad\dfrac{3\sqrt y}{\sqrt 2}-\dfrac{1}{\sqrt 2}=0\\\\ \sqrt{2x} =\dfrac{1}{\sqrt 2}\quad\quad\;\;\; \quad\quad\quad\quad\dfrac{3\sqrt y}{\sqrt 2}=\dfrac{1}{\sqrt 2}\\\\ 2x =\dfrac{1}{2}\quad\quad\quad\quad\;\;\quad\quad\quad\quad\dfrac{9y}{2}=\dfrac{1}{2}\\ \\ x=\dfrac{1}{4} \quad\quad\quad\;\;\quad\quad\quad\quad\;\;\quad y=\dfrac{1}{9}$