1. Алгебра
  2. Комплексное число (корень

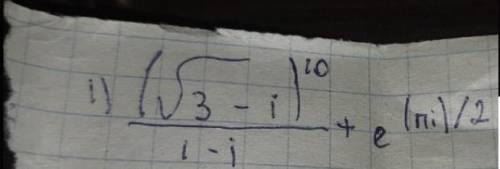
Комплексное число (корень 3 - i)^10 / 1 - i


Комплексное число (корень 3 - i)^10 / 1 - i

Mаjоr Mаjоr    3   25.06.2021 20:38    0

Ответы
  25.07.2021 21:01

Объяснение:

\frac{(\sqrt{3} -i)^{10}}{1-i} +e^{i\pi /2}

Разберем по порядку. Сначала возведем скобку в степень.

Для этого представим скобку в тригонометрической форме:

\sqrt{3} -i= 2(\frac{\sqrt{3} }{2} -\frac{1}{2}*i )=2(cos(\frac{11\pi }{6} )+i*sin(\frac{11\pi }{6} ))

Возводим это в степень:

[2(cos(\frac{11\pi }{6} )+i*sin(\frac{11\pi }{6} ))]^{10}=2^{10}(cos(\frac{110\pi }{6} )+i*sin(\frac{110\pi }{6} ))=

=1024(cos(\frac{(108+2)\pi }{6} )+i*sin(\frac{(108+2)\pi }{6} ))=1024(cos(\frac{2\pi }{6} )+i*sin(\frac{2\pi }{6} ))=

=1024*(cos(\frac{\pi }{3} )+i*sin(\frac{\pi }{3} ))=1024*(\frac{1}{2} +\frac{\sqrt{3} }{2} *i)=512(1+\sqrt{3}*i )

Теперь делим. Умножаем числитель и знаменатель на комплексно-сопряженное число:

\frac{512(1+\sqrt{3}*i )(1+i)}{(1-i)(1+i)} =\frac{512(1+\sqrt{3}*i+i+\sqrt{3}*i^2)}{2} =256(1-\sqrt{3} +i*(1+\sqrt{3} ))=

=256(1-\sqrt{3} )+(256+256\sqrt{3})*i

И последнее слагаемое. Есть известное равенство:

e^{i\pi }=-1

Отсюда

e^{i\pi /2}=\sqrt{e^{i\pi }} =\sqrt{-1} =i

Складываем:

256(1-\sqrt{3} )+(256+256\sqrt{3})*i + i = 256(1-\sqrt{3} )+(257+256\sqrt{3})*i

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
annsamoilenko16 annsamoilenko16  17.11.2020 17:50
решить. Область определения функции...
Боббоянн Боббоянн  17.11.2020 17:50
Я не понимаю Что тут делать !...
dodess dodess  17.11.2020 17:51
менша основа рівнобічної трапеції дорівнює 10 см, знайдіть більшу основу трапеції, якщо висота, проведена з вершини тупого кута, ділить її на відрізки, один із яких дорівнює 3 см​...
Philap Philap  17.11.2020 17:51
Замість зірочки запишіть такий многочлен, щоб утворилася тотожність:% - зірочка ​...
Mandarinka0001 Mandarinka0001  02.12.2020 01:40
1) Найдите площадь параллелограмма, если две его стороны равны 6 см и 8 см, а один из углов равен 150 о . 2) Найдите площадь треугольника, две стороны которого равны 12 см и 9 см,...
EsMiLe1999 EsMiLe1999  02.12.2020 01:22
Равнобедренные треугольники описаны около квадрата со стороной а так, что одна сторона квадрата лежит на основании треугольника. Обозначая ВК = х, найти такое значение х, при котором...
Mamishbdjsnb Mamishbdjsnb  20.12.2020 18:30
Решите уравнения: а) sin x =√2 b) cos x=√3...
Milka210413 Milka210413  20.12.2020 18:30
Функция задана формулой f(x) = -3х3f(3) =f-4) = ​...
StarAl73 StarAl73  20.12.2020 18:30
6(x^2-4)-4x(x+3)=2x^2 решите уравнение) ​...
mafobe66 mafobe66  20.12.2020 18:30
Cos(65°)+sin(205°)= 0 почему 0 ?​...

Популярные вопросы