Комбинаторика
1) Шестнадцать студентов разделились на две равные группы, каждая из 8 студентов соответственно, для поиска на местности объекта, который их интересовал. Только 4 из них были знакомы с местностью. Сколькими они могут распределиться таким образом, чтобы в каждой группе было по два студента, которым знакома местность?
2) Собрание студенческой группы, состоящей из 20 человек (среди них две девушки), выбрали делегацию из 6 человек на студенческую конференцию. Сколько может существовать формирования делегации, в которой присутствуют обе девушки?
3) Студенческий комитет для первокурсникам предоставил группу студентов со старших курсов, состоящая из 5 человек. Отбор проводили с 20 добровольцев, среди которых было 5 огудентив с шестого курса и 4 с пятого. Количество комплектаций группы возможна, если к ней обязательно входит по одному студенту из шестого и пятого курса?
Другие вопросы по теме Алгебра
Популярные вопросы
- Назовите любые три структурных компонента политической системы и...
1 - 17370: 45*67=25862 540*72: 40: 9=108 36075: 37*25=24375 39900: 25*12=19152...
2 - Скылки хвилин стеновить одна шоста години? ?...
3 - Поиск результатов по фразе где не можешь пока объяснить выбор букв...
1 - Сколько существует различных трёх значных чисел, в записи которых...
2 - Вычислите (-4)в минус 3 степени; 2,5 в минус 1 степени...
1 - Які два числа треба вставити між числами 3 і -192, щоб вони разом...
3 - Нужно 1) как найти массу калий карбоната который нужен для 200 гр...
1 - Решите уравнения : 45: (x-5)=15 (x+3)*3=27 (x-4): 5=7 (x+5): 3=15...
3 - Мне нужно сочинение на французском про лучшую подругу. с переведом....
1
Пошаговое объяснение:
1. т.к. мы выбирая первую группу автоматом получаем вторую, то можно считать сколько выбрать первую группу
нам надо выбрать двух знающих, и остальных 6 из незнающих
2.
две девушки точно входят, осталось выбрать еще 4 человека из оставшихся 18
3.
выбираем одного с пятого, одного с шестого и остальных трех с 11 оставшихся:
1) 5544
Объяснение:
Число сочетаний из n по k это биномиальный коэффициент, вычисляемый по формуле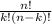 . Где к!=1·2·3·...·к. Исключение 0!=1
. Где к!=1·2·3·...·к. Исключение 0!=1
1) Число сочетаний из 4 по 2 будет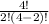 =6
=6
Число сочетаний из 12 по 6 будет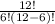 =924
=924
6·924=5544