1. Алгебра
  2. Катер развивающий скорость

Катер развивающий скорость в стоячей воде 20 км/ч км против течения и 22 км по течению затратив на весь путь 3 часа. найти скорость течения реки?

Dasha555511111 Dasha555511111    2   16.03.2019 22:50    1

Ответы
milenabalayan milenabalayan  25.05.2020 17:32

Решение. Пусть, скорость течения реки - х.

Тогда скорость катера будет:

ПО течению - 20+х

Против течения - 20-х, км/ч.

Пусть, t - время движения по течению.

Тогда время движения против течения будет = (3-t)

Запишем условия в виде уравнений:

(20+x)*t=36

(20-x)*(3-t)=22

\left \{ {{(20+x)t=36} \atop {(20-x)(3-t)=22} \right. \ \ \ \left \{ {{t=\frac{36}{20+x}} \atop {(20-x)(3-\frac{36}{20+x})=22} \right. \ \

Решим второе уравнение системы.

(20-x)(3-\frac{36}{20+x})=22} \ \ <= \ \ (20-x)(\frac{60+3x-36}{20+x})=22

(20-x)(\frac{60+3x-36}{20+x})=22\ \ \ <=\ \frac{(20-x)(24+3x)}{20+x}=22

Преобразуем в квадратное уравнение:

480+60x-24x-3x^2=440+22x

40+14x-3x^2=0

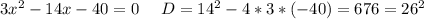
40+14x-3x^2=03x^2-14x-40=0 \ \ \ \ D=14^2-4*3*(-40)=676=26^2

x=(14+-26)/6

x=(14+26)/6=40/6=6+2/3

X2<0, что противоречит условиям

 Отсюда получаем, что 

x=\frac{20}{3}=6\frac{2}{3}

 

ответ: скорость течения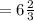 =6\frac{2}{3} км/час

 

Проверка:\frac{36}{20+\frac{20}{3}}+\frac{22}{20-\frac{20}{3}}=</p&#10;<p[tex]=\frac{36*3}{60+20}+\frac{22*3}{60-20}=

=\frac{108}{80}+\frac{66}{40}=

\frac{108+132}{80}=3 часа

 
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
larisa115 larisa115  22.07.2019 03:00
Найдите сумму корней уравнения 5х^2 +3х-2=0...
Anonim307 Anonim307  22.07.2019 03:00
Если сторону квадрата уменьшить на 4м, то получится квадрат, площадь которого меньше площади первоначального квадрата на 96м2. найдите площадь квадрата....
Татьяна72828 Татьяна72828  22.07.2019 03:00
Решите ! 2⁹ / 2⁷ × 32 в числителе 2⁹ в знаменателе 2⁷ × 32...
snezanakoba snezanakoba  22.07.2019 03:00
Решите графическое уравнение x2=x+2...
Ильсяс Ильсяс  30.09.2019 03:50
Велосипедист за 3 часа может проехать такое расстояние, какое пешеход — пройти за 8 часов, т. к. скорость пешехода на 7 км/ч меньше. найдите скорость велосипедиста....
St9747 St9747  30.09.2019 03:50
Туристы маршрут длиной 46 км. часть пути они шли пешком, а часть - ехали на верблюдах. сколько километров они пешком, если на верблюдах ехали на 15 км больше. решить...
Vrronika778 Vrronika778  30.09.2019 03:50
Найдите заначение выражений -3+0,4x и -4+0,5x при х=7...
alinkass alinkass  30.09.2019 03:50
Какая цифра стоит на 59 м месте после запятой в числе 0,5(641); 1) 5; 2) 4; 3) 6; 4) 1....
SkiJu SkiJu  30.09.2019 03:50
Это дробь если что. решить 5у-4/21 - 6-2у/14 = 4у+1/7...
hamestik hamestik  30.09.2019 03:50
Представте дробь 4/11 в виде переодической десятичной дроби....

Популярные вопросы