Какая прямая является осью симметрии параболы у=ах^2+bx+c в зависимости от значения а?

Ответы

annuwka1 25.12.2020 01:32

y=ax^2+bx+c

Осью симметрии параболы является прямая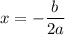 $x=-\dfrac{b}{2a}$ .

Получить это можно, выполнив преобразование:

$ax^2+bx+c=a\left(x^2+\dfrac{b}{a} x+\dfrac{c}{a} \right)=$

$=a\left(x^2+2x\cdot\dfrac{b}{2a}+\left(\dfrac{b}{2a}\right)^2-\left(\dfrac{b}{2a}\right)^2+\dfrac{c}{a} \right)=$

$=a\left(\left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2}{4a^2}+\dfrac{4ac}{4a^2} \right)=a\left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2}{4a}+\dfrac{4ac}{4a} =$

$=a\left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2-4ac}{4a}=a\left(x-\left(-\dfrac{b}{2a}\right)\right)^2-\dfrac{b^2-4ac}{4a}$

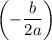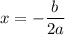Горизонтальный сдвиг осуществляется на $\left(-\dfrac{b}{2a}\right)$ вправо. Значит, прямая $x=-\dfrac{b}{2a}$ является осью симметрии параболы.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

penina1 19.08.2019 15:20

Решите уравнение (5x^2)^3*(2x^3)^5=2^2*10^3...

KirochkaMirina 19.08.2019 15:20

Изобразите на координатной плоскости множество точек, удовлетворяющих условиям: у = х3 и |х| ≤4....

RIF12 19.08.2019 15:20

Y=0,5x+4 y=-3x-2 найдите точку пересечения...

doroxova04 19.08.2019 15:20

Решите систему уравнений: {x+y=70 {40²+x²=30²+y²...

15gallagher 19.08.2019 15:10

1.найдите корни уравнения. (x+1)/(2x+3)=(3x+2)/(x+1) 2. решение системы неравенств |x-1| =3 |x+3| =2 = - меньше или равно...

gri6anja20021 19.08.2019 15:10

Выполните преобразование по соответствию формуле: а)(4+а)^2 б)(4х+у)^2 в)(2а-1)^2 г)(х-12)^2 д)(а^2-2b)^2 e)(8x+y^2)^2...

Lanatm12 19.08.2019 15:10

Изменится ли значение выражения: 0^n, (-1)^n, (-1)^2n если число n увеличить на один ?...

Roma99812 19.08.2019 15:10

Найдите шестой член прогрессии (bn)если b1=0.81? g=1/3...

roslanova051 04.05.2020 16:00

решить {7х+3y=43 {4x-3y=67...

Graffiti1337 04.05.2020 16:00

20x^2-12x+1 -- разложите на множители квадратный трехчлен...

Какая прямая является осью симметрии параболы у=ах^2+bx+c в зависимости от значения а?

Популярные вопросы