Какая из двух показательных функций возрастает быстрее при возрастании значений аргумента: y = 2^x или y = (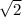)^2

Добрый день, давайте разберем этот вопрос.

Первая функция: y = 2^x
Вторая функция: y = (√2)^x

Мы хотим определить, какая из этих двух функций возрастает быстрее при возрастании значений аргумента.

Для начала, давайте построим графики обеих функций. Это поможет нам визуально увидеть, как они меняются.

1. График функции y = 2^x:
Для построения графика этой функции, мы можем выбрать несколько значений аргумента x и расчитать соответствующие значения функции y.

Например:
- x = 0, y = 2^0 = 1
- x = 1, y = 2^1 = 2
- x = 2, y = 2^2 = 4
- x = 3, y = 2^3 = 8

Получив эти значения, мы можем построить график функции y = 2^x, используя координатную плоскость. График будет проходить через точки (0, 1), (1, 2), (2, 4) и (3, 8). Изобразив эти точки и соединив их плавной кривой, мы получим график функции y = 2^x.

2. График функции y = (√2)^x:
Аналогично, для построения графика этой функции, мы выбираем несколько значений аргумента x и расчитываем соответствующие значения функции y.

Например:
- x = 0, y = (√2)^0 = 1
- x = 1, y = (√2)^1 ≈ 1.414
- x = 2, y = (√2)^2 ≈ 2
- x = 3, y = (√2)^3 ≈ 2.828

Получив эти значения, мы можем построить график функции y = (√2)^x, используя ту же координатную плоскость. График будет проходить через точки (0, 1), (1, 1.414), (2, 2) и (3, 2.828). Подобно предыдущему графику, мы соединяем эти точки плавной кривой, чтобы построить график функции y = (√2)^x.

Теперь мы можем сравнить оба графика и определить, какая функция возрастает быстрее. Обратите внимание, что по графику, значения функции y = (√2)^x растут медленнее, чем значения функции y = 2^x.

Есть также аналитический способ сравнить рост этих функций. Давайте напишем обе функции в эквивалентной форме:

1. Функция y = 2^x: эта функция может быть записана как y = e^(x * ln(2)), где e - экспонента (приблизительно 2.71828), ln - натуральный логарифм.
2. Функция y = (√2)^x: эта функция может быть записана как y = e^(x * ln(√2)).

Теперь, мы должны сравнить два показателя в вышеуказанных функциях, то есть x * ln(2) и x * ln(√2).
Рассмотрим каждое из них:

- x * ln(2): в этом случае, мы умножаем значение x на константу ln(2). Константа ln(2) - положительное число, и поэтому, когда x возрастает, произведение x * ln(2) также возрастает. Это означает, что функция y = 2^x возрастает при увеличении аргумента x.

- x * ln(√2): в этом случае, мы умножаем значение x на константу ln(√2). Поскольку ln(√2) - отрицательное число, когда x возрастает, произведение x * ln(√2) убывает. Это означает, что функция y = (√2)^x убывает при увеличении аргумента x.

Таким образом, оба графика и аналитический подход показывают, что функция y = 2^x возрастает быстрее, чем функция y = (√2)^x при увеличении значений аргумента.

Надеюсь, данное пояснение было понятным для вас. Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задавать их. Я всегда готов помочь.