Какая формула для нахождения sin4a; cos4a и ctg4a?
Другие вопросы по теме Алгебра
Популярные вопросы
- решить задачи по физике. Камень падает вертикально вниз без начальной...
3 - Natural wonders of the world Click the correct option to identify the...
1 - ДИДАКТИЧЕСКИЙ МАТЕРИАЛ ПО РУСС. 4 КЛАСС Перед тобой наборы букв. Составь...
3 - Вычеслите 11*(-17)+15*(-31)...
2 - Измените число выделенного существительного, где возможно и выполните...
1 - 2. These sentences are from a dialogue between two friends. Saythem in...
2 - Х Почему обачество располось вкраса іѕ а белых1 Красная армия е верува...
3 - Салтанат заплатил 17 лир и купил два вида конфет, каждый по килограмму....
3 - ааа с этим ну быстрее умоляю ну быстрее двлвлуллкклклк мне щяс потом...
1 - Мамандықтың жаманы жоқ деген тақырыпта шағын мәтін жазыңдар.Мәтінде...
1
1. Так как , то данный угол первой четверти и все тригонометрические функции в ней положительны.
, то данный угол первой четверти и все тригонометрические функции в ней положительны.
2, Так как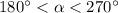 , то данный угол третьей четверти, синус и косинус в ней отрицательны.
, то данный угол третьей четверти, синус и косинус в ней отрицательны.