1. Алгебра
  2. Как возвести комплексное

Как возвести комплексное число в 24 степень с формулы муавра?

Lyuda56 Lyuda56    1   28.09.2019 18:50    0

Ответы
1234567891252 1234567891252  16.08.2020 23:59

\left(1+\frac{\sqrt{3}}{2}+\frac{i}{2}\right)^{24}=\left(1+\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}\right)^{24}=\left(2\cos^2\frac{\pi}{12}+2i\sin\frac{\pi}{12}\cos\frac{\pi}{12}\right)^{24}=

=\left(2\cos\frac{\pi}{12}\left(\cos\frac{\pi}{12}+i\sin\frac{\pi}{12}\right)\right)^{24}=2^{24}\cos^{24}\frac{\pi}{12}\left(\cos\frac{24\pi}{12}+i\sin\frac{24\pi}{12}\right)=

=2^{24}\left(\cos^2\frac{\pi}{12}\right)^{12}\left(\cos2\pi+i\sin 2\pi\right)=2^{24}\cdot\left(\frac{1+\cos\frac{\pi}{6}}{2}\right)^{12}(1+0i)=

=2^{24}\cdot\frac{(1+\sqrt{3}/2)^{12}}{2^{12}}=2^{24}\cdot\frac{(2+\sqrt{3})^{12}}{2^{24}}=(2+\sqrt{3})^{12}

Думаю, что это и есть предполагаемый ответ, поскольку возвести двучлен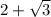 2+\sqrt{3} в 12-ю степень с бинома Ньютона, конечно, можно, но довольно утомительно.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ученик11111023531 ученик11111023531  12.07.2019 16:30
4х²-5х =0 является ли 1,2 корнем уравнения...
cvetaharlanova5 cvetaharlanova5  12.07.2019 16:30
Тело движется равномерно и промолинейно со скоростью 54 км/ч. чему равна скорость тела ,выраженная в м/с....
tinafortinova78 tinafortinova78  12.07.2019 16:30
Найти значение выражений x в квадрате +6=5x...
dasha54321d dasha54321d  12.07.2019 16:30
Найдите значение выражения корень из(12-6 корней из 3) + корень из (19+8 корней из 3)...
Sanya030814 Sanya030814  12.07.2019 16:30
Выражение (3 х^2 y)^3*5 у ^7 в стандартном виде...
kiradimitrova kiradimitrova  08.04.2019 20:06
Решить 4 вариант по кроме 6 номера и все подробно...
Fluttershy22102005 Fluttershy22102005  08.04.2019 20:06
Сделайте все кроме 3 плеаз надо...
chechia chechia  08.04.2019 20:06
Сократите дробикто тому сало​...
Alena11094 Alena11094  08.04.2019 20:00
Найдите четырёхзначное число, крат­ное 18, про­из­ве­де­ние цифр ко­то­ро­го равно 64. в от­ве­те ука­жи­те какое-нибудь одно такое число....
Tosya03 Tosya03  08.04.2019 19:59
Вычеркните в числе 67801349 три цифры так, чтобы получившееся число делилось на 6. перечислите все варианты. в ответе укажите какое-нибудь одно такое число....

Популярные вопросы