1. Алгебра
  2. Как решить такой интеграл?

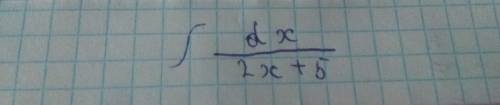
Как решить такой интеграл? (с объяснением)


Как решить такой интеграл? (с объяснением)

spark74 spark74    1   05.09.2021 21:01    0

Ответы
mariamadaeva mariamadaeva  14.11.2021 23:38

Объяснение:

Анализируем подынтегральную функцию.

\int \frac{dx}{2x + 5}

Здесь у нас дробь,

\frac{1}{2x + 5}

в знаменателе которой - линейная функция 2х+5.

В таблице интегралов и наиболее похожая вещь:

\int \frac{dx}{x} = \ln |x| + C

Подводим эту линейную функцию под знак дифференциала:

\small\int \frac{dx}{2x + 5} = \int \frac{ \tfrac{1}{2} \cdot2 dx}{2x + 5} = \small \frac{1}{2} { \int} \frac{2 dx}{2x + 5} = \\ = \frac{1}{2}{ \int }\frac{ d(2x)}{2x + 5} = \frac{1}{2} {\int} \frac{ d(2x + 5)}{2x + 5} = ...

Далее используем табличную формулу, где у нас вместо х - выражение 2х+5:

...= \frac{1}{2} {\int} \frac{ d(2x + 5)}{2x + 5} = \frac{1}{2} \cdot \ln |2x + 5| + C \\

Получаем ответ:

\int \frac{dx}{2x + 5} = \frac{1}{2} \ln |2x + 5| + C \\

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ianastepanenko ianastepanenko  18.08.2019 15:40
X^2+3x-10/x+3 найти нули функции и область ее определения...
scravtz scravtz  18.08.2019 15:40
1)4c^2-49b^2 2)x^2y^2 3)144-49n^2 4)p^2q^2-4k^2 !...
AiDanttlll AiDanttlll  24.04.2020 12:56
3x+2y=4. Выразите из данного уравнения переменную х через у. В преобразованном выражении при необходимости сократите дроби, не выделяя целую часть. ответ запишите английскими...
alholod2p00me0 alholod2p00me0  24.04.2020 12:56
решите арифметическую и геометрическую прогрессию...
lGeneralll lGeneralll  24.04.2020 12:56
В растворе содержится 20 % соли. Если добавить 120 г соли, то в растворе будет содержаться 40 % соли. Сколько граммов соли было в растворе первоначально? ответ: г. Полученное...
Yana05050 Yana05050  09.10.2021 07:47
Студент приготовил к экзамену 50 вопросов из 60. В 30 билетах вопросы распределены случайным образом. Для положительной оценки надо ответить хотя бы на один из двух вопросов...
jhghjlkuyfjy jhghjlkuyfjy  09.10.2021 07:48
РЕШИТЕ ! 10) bu = -0.36 11) -12k = -1.44 12) -0.2x = -1.2 13) 1.7y = -0.34 14) -7.4m = -1.48 15) 3x = 1 16) 7r = -4 17) 13y = -10 18) -10v = -7...
Дима99999910 Дима99999910  09.10.2021 07:50
5⁸×(5⁴)⁵5²⁵ комектесындерш...
AnastasiyaSm AnastasiyaSm  09.10.2021 07:50
1/2а^2в^4х×3/4 при а=2, b=1, x=1/2...
krasava5vovan krasava5vovan  09.10.2021 07:54
Алгебра , ток норм ответить...

Популярные вопросы