Как решать показательные неравенства? ​

т.к.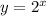 - показательная функция, основание больше 1, т.е. 2>1.

То знак НЕ меняется.

Введём функцию: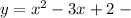 квадратичная функция, график парабола, ветви вверх, т.к. коэффициент при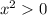

2) Найдём область определения функции:

3) Найдём корни уравнения, т.е.

Решая методом интервалов, находим, что решение выглядит так: