Как решать квадратные уравнения?

Коли просите, не могу отказать ;) Я дам только решение, без доказательств и тонкостей, все это можно найти в интернете при должном желании.

x² + px + q = 0 - приведенное квадратное уравнение

Теорема Виета гласит, что произведение корней приведенного квадратного уравнения равно свободному члену (q), а их сумма равна числу обратному второму коэффициенту (-p)

x₁ · x₂ = q

x₁ + x₂ = -p

Часто нам будут даваться не приведенные квадратные уравнение, а обычные, они имеют вид

ax² + bx + c = 0 (то же приведенное, но с коэффициентом перед x-ом)

что бы получить из обычного квадратного уравнение приведенное, нужно разделить его на a. От сюда сумма и произведение корней обычного квадратного уравнения равны:

x₁ · x₂ =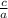

x₁ + x₂ = -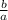

Пример:

x² - 4x + 3 = 0

Тогда корни:

x₁ = 1

x₂ = 3

Надеюсь, что все понятно)