Как находить производную? (напишите как именно) примеры (5-10), с легких до чутьболее сложных примеры для решения мне (5-10) - решение не писать, только условие и ответ
Другие вопросы по теме Алгебра
Популярные вопросы
- решить пример. Интегралы. Есть сам пример и ответ какой должен...
3 - ответить на вопросы, хотя бы на какие сможете Задание 1 Вопрос:...
3 - Как найти последние 4 цифры номера телефона. 8777368...
1 - 1 Қос теңсіздіктің шешімдер жиынын табааламын және түсінемін.а)...
1 - Решите пример 25-19*(-5)=25+15*(-5)=...
1 - На какой вопрос отвечает слово Лекциям?...
3 - Установить вiдповiднiсть мiж назвою католицького ордену та стислою...
2 - Русский язык Выполни упражнение 484, стр.263 (письменно)....
3 - Надо еще составить обратные задачи помагите НАДО...
1 - Востановите частично стертые записи:...
2
Нахождение проивзодной называют дифференцированием. Знак дифференцирования - ` (штрих).
Производную находят по формулам:
Правила дифференцирования:
Примеры:
Решить:
1)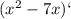
2)
3)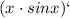
4)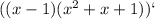
5)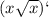
6)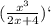
7)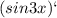
8)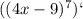
ответы:
1)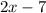
2)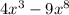
3)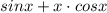
4)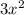
5)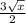
6)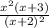
7)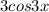
8)