K-ның қандай мәндерінде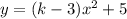
функциясының графигі а) парабола ә)түзу болады. көмектесіңіз дерші​

Хорошо, давайте разберем этот вопрос поэтапно.

Первым делом давайте разберемся, что означает данная функция y = (k - 3)x^2 + 5.

Это функция представляет собой уравнение параболы. Парабола - это график квадратичной функции, которая имеет форму укачивающего ногами вверх или вниз параболического арки.

В данном уравнении x^2 означает, что значение x, возведенное в квадрат.

Теперь, чтобы выяснить, будет ли график параболы узким или широким, нужно рассмотреть коэффициент k, который стоит перед x^2.

Этот коэффициент k влияет на форму и конкретную позицию параболы на графике. Таким образом, чтобы понять, какая будет форма параболы в зависимости от значения k, нужно оценить его влияние на график.

а) Если k > 0, то парабола будет узкой и открытой вверх. Это означает, что увеличение значения x приведет к увеличению значения y. График будет иметь ветви, направленные вверх.

б) Если k < 0, то парабола будет узкой и открытой вниз. Это означает, что увеличение значения x приведет к уменьшению значения y. График будет иметь ветви, направленные вниз.

Таким образом, форму параболы можно определить на основании значения k перед x^2.

Для решения данной задачи вам нужно определить, какие значения k будут делать параболу узкой и открытой вверх (а) и какие значения делают ее узкой и открытой вниз (б).

Приравняем k - 3 к 0 и решим это уравнение:

k - 3 = 0,

k = 3.

Таким образом, при k = 3 парабола будет иметь форму б - узкую и открытую вниз.

Исходя из этого, можно сделать вывод, что для всех значений k, кроме 3, график функции будет иметь форму а - узкую и открытую вверх, а при k = 3 график будет иметь форму б - узкую и открытую вниз.