Известно, что sin = 8/17, 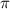 /2< a <
/2< a <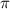 . Найдите значения трех других тригонометрических функций угла тригонометрического тождества.
. Найдите значения трех других тригонометрических функций угла тригонометрического тождества.
Другие вопросы по теме Алгебра
Популярные вопросы
- Ширина прямоугольника равна 81 см что составляет 79длина Найдите площадь прямоугольника...
2 - Exercise 6. Определите подлежащее и сказуемое в предложениях и переведите...
2 - Moscow CircusesMost people are greatly fond of circus. Russian circus and...
1 - 1) Запишите квадратное уравнение, в котором: 1) Старший коэффициент равен...
3 - Артур Конан Дойл. Оповідання Собака Баскервілів . Скласти до нього план....
2 - - Подготовить доклад по теме: «Олимпийское движение в России» Объем доклада...
1 - Put the verbs into the correct Future Continuous formPut the verbs in brackets...
2 - Какую работу совершает ток в электродвигателе пылесоса за 25 мин, если сила...
3 - Red SquareThe heart of Moscow is Red Square. And the heart of Red Square is...
1 - 1.У Антона есть 80 гирь с весами 1 г, 2 г, 3 г, ..., 80 г. Сколько из этих...
3
α - угол второй четверти значит Cosα < 0 , tgα < 0 , Ctgα < 0 .