Известно,что графики функций у=-х2+р и у=-2х+2 имеют ровно одну общую точку.определите координаты этой точки.постройте графики функций в одной системе координат

Первый геометрический смысл производной)

Производная в точке равна угловому коэффициенту касательной к графику функции 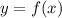в этой точке.

Пусть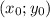 - точка касания двух графиков. Тогда

y = -2x + 2 - касательная к графику y = -x² + p  ⇒   k = -2

Производная функции: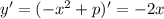

Используя геометрический смысл производной, мы получим

Получили абсциссу точку касания, тогда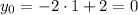

Тогда, подставив точку (1;0) в первый график уравнения, найдем р

При р = 1 имеется общая точка (1;0) графика функции y = -x² + 1 и прямой y = -2x + 2.

y = -x² + 1 - парабола, ветви которой направлены вниз. Вершина параболы (0;1). Точки построения изображены на картинке.

y = -2x + 2 - прямая, проходящая через точки (0;2), (1;0).

Второй Определение через дискриминант)

Приравниваем функции: -x² + p = -2x + 2 или -x² + 2x + p - 2 = 0

D = b² - 4ac = 4 + 4(p-2) = 4(1 + p -2) = 4(p-1)

Чтобы графики имели одну общую точку, достаточно чтобы квадратное уравнение имело одно единственное решение, т.е. когда D = 0.

4(p-1) = 0

p = 1.

При р = 1, получим -x² + 2x + 1 - 2 = 0  ⇔  -(x-1)² = 0   ⇒  x=1

y = -1² + 1 = 0

Координаты точки касания двух графиков (1;0).