Известна площадь циферблата Кремлёвских курантов. Как найти радиус и диаметр курантов класс
Заранее
Другие вопросы по теме Алгебра
Популярные вопросы
- Завершите этот телефонный разговор правильной настоящей совершенной...
3 - Решите уравнение 5(х-1,2)-3х решите ❤️...
2 - Нужно нарисовать часы в программе кумир...
2 - Какой случай в жизни героя сыграл особую роль в формировании его личности?по...
1 - с алгеброй контрольная (не для меня) с решением...
3 - Приведи подобные слагаемые: −2,38x+7,5x−19,3x. ответ (записывай ответ...
3 - Яким постає ліричний герой вірша Бернса?Як він характеризує свою батьківщину...
2 - с русским языком 7 класс! Внимательно прочитайте задание на картинке...
2 - Какие ансамблевые номера (по числу участников) вы можете назвать...
1 - Какой математический знак нужно поставить между цифрами 8 и 5 чтобы...
3
Объяснение:
S=П*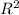 , где П=3.14 (число пи) а R-радиус
, где П=3.14 (число пи) а R-радиус
следовательно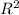 =S:П
=S:П
R=x (из деления) или R=-x (не удовл. тк.к радиус не может быть отрицательным)
d=2R=2*x(значение которое мы нашли)
Пусть площадь циферблата Кремлевских курантов равна S. Мы знаем, что форма циферблата круглая, поэтому его площадь можно найти по формуле:
S = π * r^2,
где r - радиус круга, π - математическая постоянная, примерное значение которой равно 3.14 или 22/7.
Чтобы найти радиус r, нужно выразить его из формулы площади:
r = √(S / π).
Теперь, если у нас есть значения площади S, мы можем подставить их в формулу и найти радиус.
А диаметр круга (d) - это просто удвоенное значение радиуса (r), то есть:
d = 2 * r.
Таким образом, если мы найдем радиус, мы сможем найти и диаметр.
Давайте проверим это на примере. Пусть площадь циферблата Кремлевских курантов равна 100 квадратных сантиметров.
1. Выразим радиус из формулы площади:
r = √(100 / π).
2. Подставим значение π (3.14) и рассчитаем радиус:
r = √(100 / 3.14) ≈ √31.8471 ≈ 5.6437.
3. Теперь, найдя радиус, можем найти диаметр:
d = 2 * r ≈ 2 * 5.6437 ≈ 11.2874.
Итак, по нашим расчетам, радиус курантов примерно равен 5.6437 сантиметра, а диаметр - 11.2874 сантиметра.
Надеюсь, я смог пошагово объяснить, как найти радиус и диаметр курантов. Если у вас возникнут еще вопросы, пожалуйста, задайте их. Удачи в изучении математики!