Изменить порядок интегрирования в двойном интеграле.Сделать чертеж.
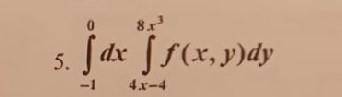
Другие вопросы по теме Алгебра
Популярные вопросы
- Какую функцию выполняет корневой волосок...
2 - По какому слову в сложносокращенном слове определяется род?...
2 - 1вопрос)запишите на языке. периметр треугольника авс равен 49 см, сторона...
2 - Удвух друзей 16 солдатиков.если один даст другому одного солдатика то у них...
1 - Два оператора набирали на компьютере текст рукописи. один выполнил 70% работы,...
3 - Ділене дорівнює 99, неповна частка 7, остача 8. як знайти дільник? дякую!...
1 - Социологические теории современности. — м., 1992 — с. 42–43 и ответьте на...
3 - Как вы понимате смысл выражения нужно принять себя таким, какой ты есть...
2 - Полуостров, бывший до 19 в. самая крупная система пещер мира южная америка...
1 - Чому коли футболіст б є м яч він летить по криволінійній лінії?...
1
Обратимся к рисунку. Видим, что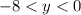 .
.
Причём, пока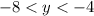 , переменная
, переменная  меняется от
меняется от ![x=\dfrac{\sqrt[3]{y}}{2}](/tpl/images/1855/6786/5969b.png) до
до  .
.
Когда же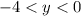 , то
, то  меняется от
меняется от ![x=\dfrac{\sqrt[3]{y}}{2}](/tpl/images/1855/6786/5969b.png) до
до 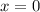 .
.
Таким образом,