Из города а в город в одновременно выехали автомобиль и мотоцикл а в тот момент, когда мотоцикл преодолел шестую часть пути, из а в том же направлении выехал велосипедист. к моменту прибытия автомобиля в город в велосипедист проехал четвертую часть пути. скорость мотоцикла на 21 км/ч меньше скорости автомобиля и на столько же же больше скорости велосипедиста.найти скорость автомобиля.

ответ: 63 км/ч.

Объяснение: Пусть расстояние от города А до города В 1 (единица), х км/ч скорость автомобиля, тогда скорость мотоцикла будет х-21 км/ч, а скорость велосипедиста х-21-21 = х-42 км/ч. Время, которое автомобилист затратил на весь путь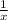 часов, время которое мотоциклист затратил на 1/6 часть пути 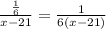часов, а велосипедист на 1/4 часть пути затратил 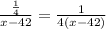часов или затратил 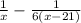часов. Составим уравнение:

x₁=24 (км/ч) не подходит. т.к. скорость велосипедиста будет 24-42=(-18) (км/ч) (отрицательная), что противоречит условию задачи.

x₂=63 (км/ч) скорость автомобиля.