Исследуйте функцию с производной и постройте график
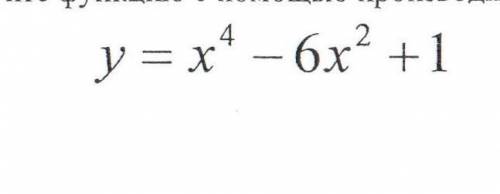
Другие вопросы по теме Алгебра
Популярные вопросы
- Чем отличается сперматозоид от яйцеклетки?...
2 - Разложите на множители: 1. а(х+у) - b(x+y) 2. x(x+4) - y(x+4) 3. b(x-3)...
2 - На одной машине 6 мешков моркови,а на другой 10 таких же мешков .масса...
2 - Роман, павел и сергей на компьютере вместе набрали 3700 очков. сколько...
2 - Сравнить дроби: 3/16 и 19/42 и 3/6...
2 - 15148разделить на4 покажите само решение...
1 - 20 ! найти корень уравнения log5(x+12)=log9(х+12)...
1 - Вынесите общий множитель за скобки 4y-8x...
3 - Представьте неправильные дроби в виде смешанных чисел и их к наименьшему...
2 - Охарактеризовать типы речи. примеры. первый ответ отмечу лучшим и за этот...
1
Решение задания прилагаю
от -∞ до -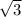 функция убывает;
функция убывает;
от -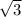 до 0 функция возрастает;
до 0 функция возрастает;
от 0 до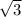 функция убывает;
функция убывает;
от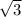 до ∞ функция возрастает;
до ∞ функция возрастает;
Объяснение:
в точках экстремума первая производная функции равна нулю.
Найдём эти точки, для этого возьмём первую производную.
y'=4x^3-12x;
приравняем к нулю.
4x^3-12x=0;
x^3-3x=0;
x(x^2-3)=0;
x1=0;
x2=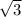 ;
;
x3=-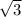 ;
;
Теперь возьмём вторую производную функции в этих точках.
y''=12x^2-12;
y''(x1)=-12 (меньше нуля, значит это точка максимума)
y''(x2)=12*3-12 (больше нуля, значит это точка минимума)
y''(x3)=12*3-12 (больше нуля, значит это точка минимума)
от -∞ до -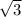 функция убывает;
функция убывает;
от -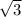 до 0 функция возрастает;
до 0 функция возрастает;
от 0 до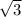 функция убывает;
функция убывает;
от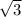 до ∞ функция возрастает;
до ∞ функция возрастает;