Исследуйте функцию и постройте её график. Именно с производной:
y=x^2-2x-3
Другие вопросы по теме Алгебра
Популярные вопросы
- Ввершинах равностороннего треугольника со стороной находятся заряды...
2 - Какие из пар (-2; 4); (-1; -3; (3; 4) является решением системы:...
2 - Найти направление линий магнит.поля ...
3 - Сделать по look at the photos a-d. complete sentences 1-4 with the...
3 - Бывшие профессиональные велосипедисты джон и ларри со- вершают длительные...
2 - Составить 2 на нахождение массы через количество вещества1.условие2....
1 - Төменде берілген қазақтың асылдары мен дара тұлғалары туралы тезис...
3 - 1.напишите формулы гидроксидов, соответствующих оксиду. названия...
1 - 25 решите квадратные уравнения: 1.3х-12х=0 2.6х-24=0 3.2х+3х+1=0...
1 - Течение 20 минут электрического шторма мария наблюдала по три удара...
1
(см. объяснение)
Объяснение:
По условию мы не знаем, что перед нами парабола.
Итак видим неизвестный науке объект:
Найдем область определения функции:
Учитывая, что функция непрерывна, найдем множество значений:
Тогда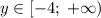 .
.
Функция не является ни четной, ни нечетной.
Определим промежутки возрастания/убывания функции:
Тогда функция убывает до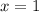 , а затем возрастает.
, а затем возрастает.
Определим выпуклость функции:
Следовательно функция выпукла вниз.
Составим таблицу для некоторых точек функции:
x|-2|-1|1 |3|4
y|5 |0|-4|0|5
Построим эскиз функции (см. прикрепленный файл).
Получилось какое-то коническое сечение с единичным эксцентриситетом.
Задание выполнено!