Исследовать сходимость ряда
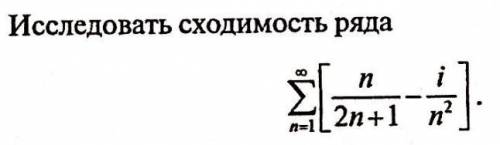
Другие вопросы по теме Алгебра
Популярные вопросы
- 31. Mum I stay out late tonight? a) Have b) can c) has...
1 - Речення за схемою: [ ] , (бо... ) : [ ]...
1 - КОРОТКО ПРИЧИНЫ ХОД ПОСЛЕДСТВИЯ гуситские войны!...
1 - створить вариацию на мелодію Р.Григорів.Варіацийи на тему укр.нар.пісні...
2 - Решите, пожайлуста1.Літак під дією сили тяги 500 кН рухається...
2 - Найдите сумму:а)-32+(-6)б)8+(-23)в)-36+36...
2 - Укажите общее число электронов в атоме с числом 25Варианты ответа:а)...
2 - Дан отрезок длины 1. Постройте отрезки с длинами а) v2; б) 3;...
3 - Я думал, что география - это какой-нибудь очень рудный предмет,...
1 - Теңқабырғалы үшбұрышқа сырттай және іштей сызылған шеңберлердің...
2
Расходится
Объяснение:
Для сходимости ряда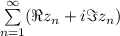 необходимо и достаточно, чтобы сходился каждый из рядов
необходимо и достаточно, чтобы сходился каждый из рядов 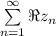 и
и 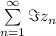
Исследуем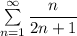
А значит и исходный ряд с комплексными членами расходится