Исследовать числовой ряд на сходимость с подробным решением

Ответы

Юля5451 13.06.2020 13:40

Для острых углов известно соотношение sinα<α<tgα . α=1/(n+6) стремится к 0 при n->∞.

tg1/(n+6)>1/(n+6).

Исходный ряд сравним с рядом ,общий член которого 1/(n+6).Этот ряд расходящийся, так как его можно сравнить с расходящимся обобщённо-гармоническим рядом ∑1/n : lim (1/n)/(1/n+6)=1≠0 при n->∞ ⇒ оба ряда ∑1/n и ∑1/(n+6) расходятся.

Ряд ∑1/(n+6) является минорантным, а ряд ∑tg1/(n+6) мажорантным. Из расходимости минорантного ряда следует расходимость мажорантного. ⇒∑tg1/(n+6) - расходящийся ряд.

ПОКАЗАТЬ ОТВЕТЫ

kioppo 13.06.2020 13:40

$\sum_{n=1}^{\infty}tg(\frac{1}{n+6})$

1) Ряд знакоположительный.

2) Применим предельный признак сравнения:

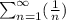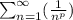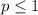Ряд $\sum_{n=1}^{\infty}(\frac{1}{n})$ - расходится (обобщенный гармонический ряд $\sum_{n=1}^{\infty}(\frac{1}{n^p})$ расходится при $p \leq 1$ )

$tg(\frac{1}{n+6}) \sim \frac{1}{n+6}, \ if \ n \to +\infty\\\\ lim_{n \to +\infty} (\frac{tg(\frac{1}{n+6})}{\frac{1}{n}}) = lim_{n \to +\infty} (\frac{\frac{1}{n+6}}{\frac{1}{n}}) =\\\\ lim_{n \to +\infty} (\frac{n}{n+6}) = lim_{n \to +\infty} (1 - \frac{6}{n+6})= 1$

Ряд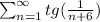 $\sum_{n=1}^{\infty}tg(\frac{1}{n+6})$ расходится согласно предельному признаку сравнения, так как ряд 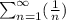$\sum_{n=1}^{\infty}(\frac{1}{n})$ расходится.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра