Используя теорему Виета 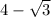
и
составьте составьте квадратное уравнение для корней
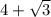
Другие вопросы по теме Алгебра
Популярные вопросы
- Составиь 5 предложений с дефисным написание предлогов...
3 - Қасықтап жинағанды дальше как? түркі айылдың батқанын дальше как? қойдан қойдың...
1 - Два пешехода вышли из 2 посёлков расстояние между которыми 48 километров и...
2 - Униколая степановича на дачном участке есть огород прямоугольной формы. ему...
1 - Запиши числовые равенства.9тысяч уменьшить на 2 тысячи....
1 - Какими правами и обязанностями обладает гражданин россии в соответствии с конституцией?...
3 - Вбудущем времени my best my brother/ sister cousin my my english my my вставить...
2 - Периметр прямо угольник 40 см .ширина равна 8 см .найди длину прямоугольника...
1 - Золотыми, разобрать слова как часть речи....
2 - Вычеркни лишнее слово ruler, subject, blue, fruit...
3
Объяснение: