Используя основное свойство дроби, найдите значение выражения: a) 10y²-3xy+20x²/8x²+xy+y², если y/x=4
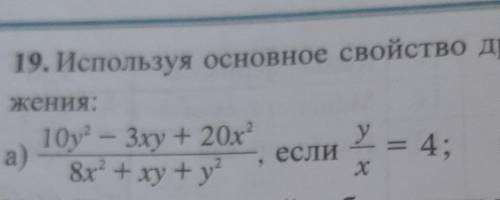
Другие вопросы по теме Алгебра
Популярные вопросы
- Определи падеж Плыли на лодке, подготовился к ответу, жили впалатке,...
3 - Из каких ветви состоит исламское религиозное течение...
3 - На рисунке 80 уголAOB=уголDOE, уголBOC=углуCOD. есть ли на этом рисунке...
3 - 2. Бағдарсызық арқылы мәтіндегі ақпараттарды мағынасымен сәйкестендіріңіз....
1 - вырази массу m квадратной пластины, сторона которой равна s см, толщина...
2 - Задание 3 Приведите примеры растений и животных, занесенных в Красную...
3 - Help написать доклад на имя Диана почиму мама и папа назвали Диана это...
3 - У прямоугольному ABCD на диагонали AC выбрана такая точка К, для которой...
2 - Автор ойын жеткізу үшін айтылу мақсатымен құрылысына қарай қандай сөйлемтүрлерін...
1 - Лёня вырезает из клетчатой бумаги квадраты 2×2, закрашивает (с одной...
2
Объяснение:
(10y^2 - 3xy + 20x^2) / (8x^2 + xy + y^2)
Делим всё на y^2
(20(x^2/y^2) - 3(x/y) + 10) / (8(x^2/y^2) + (x/y) + 1)
Если y/x = 4, то x/y = 1/4
(20*(1/4)^2 - 3*1/4 + 10) / (8*(1/4)^2 + 1/4 + 1) = (20/16 - 3/4 + 40/4) / (8/16 + 1/4 + 1) =
= (5/4 + 37/4) / (3/4 + 4/4) = (42/4) / (7/4) = 42/4*4/7 = 42/7 = 6