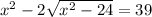 используя метод замены переменной приведите данное уравнение к виду t^2-2t-15=0
используя метод замены переменной приведите данное уравнение к виду t^2-2t-15=0
покажите что корни уравнения будут: х=±7

Ответы
Добрый день!
Для решения данного уравнения сначала приведем его к виду t^2-2t-15=0, используя метод замены переменной.
Исходное уравнение: x^{2} - 2 \sqrt{x^{2} - 24} = 39.
1. Заменим  на новую переменную t, то есть
на новую переменную t, то есть  .
Тогда наше уравнение будет выглядеть следующим образом: x^{2} - 2t = 39.
2. Возводим оба выражения уравнения в квадрат, чтобы избавиться от корня. Получаем следующее:
x^{2} = 2t + 39.
3. Теперь заменим в этом уравнении t на
.
Тогда наше уравнение будет выглядеть следующим образом: x^{2} - 2t = 39.
2. Возводим оба выражения уравнения в квадрат, чтобы избавиться от корня. Получаем следующее:
x^{2} = 2t + 39.
3. Теперь заменим в этом уравнении t на  .
Получаем: x^{2} = 2\sqrt{x^{2}-24} + 39.
4. Возводим оба выражения уравнения в квадрат еще раз:
(x^{2})^{2} = (2\sqrt{x^{2}-24} + 39)^{2}.
5. Раскрываем скобки:
x^{4} = (2\sqrt{x^{2}-24})^{2} + 2\cdot2\cdot2\sqrt{x^{2}-24}\cdot 39 + 39^{2}.
6. Упрощаем полученное уравнение:
x^{4} = 4(x^{2}-24) + 8\sqrt{x^{2}-24}\cdot 39 + 1521.
7. Далее, заменим
.
Получаем: x^{2} = 2\sqrt{x^{2}-24} + 39.
4. Возводим оба выражения уравнения в квадрат еще раз:
(x^{2})^{2} = (2\sqrt{x^{2}-24} + 39)^{2}.
5. Раскрываем скобки:
x^{4} = (2\sqrt{x^{2}-24})^{2} + 2\cdot2\cdot2\sqrt{x^{2}-24}\cdot 39 + 39^{2}.
6. Упрощаем полученное уравнение:
x^{4} = 4(x^{2}-24) + 8\sqrt{x^{2}-24}\cdot 39 + 1521.
7. Далее, заменим  на t:
x^{4} = 4(x^{2}-24) + 8t\cdot 39 + 1521.
8. Раскрываем скобки и приводим подобные слагаемые:
x^{4} = 4x^{2} - 96 + 312t + 1521.
9. Далее, упрощаем уравнение:
x^{4} - 4x^{2} + 312t - 1617 = 0.
10. Наконец, записываем это уравнение в виде t^{2} - 2t - 15 = 0, заменяя переменную x^{2} на t:
t^{2} - 2t - 15 = 0.
Мы успешно привели исходное уравнение к нужному виду.
Чтобы увидеть, что корни уравнения t^{2} - 2t - 15 = 0 равны t = 3 и t = -5, подставим значения t обратно в выражение для t, которое мы получили на первом шаге.
t = \sqrt{x^{2}-24}.
Для t = 3 получаем:
3 = \sqrt{x^{2}-24}.
Возводим оба выражения в квадрат:
9 = x^{2}-24.
Прибавляем 24 к обеим сторонам:
x^{2} = 33.
Извлекаем квадратный корень:
x = \pm \sqrt{33}.
Для t = -5 получаем:
-5 = \sqrt{x^{2}-24}.
Возводим оба выражения в квадрат:
25 = x^{2}-24.
Прибавляем 24 к обеим сторонам:
x^{2} = 49.
Извлекаем квадратный корень:
x = \pm 7.
Таким образом, мы получили, что корни исходного уравнения x^{2} - 2 \sqrt{x^{2} - 24} = 39 равны x = \pm \sqrt{33} и x = \pm 7.
на t:
x^{4} = 4(x^{2}-24) + 8t\cdot 39 + 1521.
8. Раскрываем скобки и приводим подобные слагаемые:
x^{4} = 4x^{2} - 96 + 312t + 1521.
9. Далее, упрощаем уравнение:
x^{4} - 4x^{2} + 312t - 1617 = 0.
10. Наконец, записываем это уравнение в виде t^{2} - 2t - 15 = 0, заменяя переменную x^{2} на t:
t^{2} - 2t - 15 = 0.
Мы успешно привели исходное уравнение к нужному виду.
Чтобы увидеть, что корни уравнения t^{2} - 2t - 15 = 0 равны t = 3 и t = -5, подставим значения t обратно в выражение для t, которое мы получили на первом шаге.
t = \sqrt{x^{2}-24}.
Для t = 3 получаем:
3 = \sqrt{x^{2}-24}.
Возводим оба выражения в квадрат:
9 = x^{2}-24.
Прибавляем 24 к обеим сторонам:
x^{2} = 33.
Извлекаем квадратный корень:
x = \pm \sqrt{33}.
Для t = -5 получаем:
-5 = \sqrt{x^{2}-24}.
Возводим оба выражения в квадрат:
25 = x^{2}-24.
Прибавляем 24 к обеим сторонам:
x^{2} = 49.
Извлекаем квадратный корень:
x = \pm 7.
Таким образом, мы получили, что корни исходного уравнения x^{2} - 2 \sqrt{x^{2} - 24} = 39 равны x = \pm \sqrt{33} и x = \pm 7.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Популярные вопросы
- Написать отзыв о главе кукла из повеси в.г короленко дети подземелья...
1 - Образуйте с приставок,глаголы которые можно использовать при описании игры футбол...
3 - Иутята 1. куда шли утята? 2. кого они встретили? 3. что хотели сделать с уткой?...
3 - 1) (2 б.) шкаф занесли с первого на третий этаж. при этом потенциальная энергия...
3 - Казахский язык. составте предложения с этими словами. необязательно все, можно...
3 - Мәтінмен жұмысанныңасқан. бұл қорық 1926 жылытың ұсынысымен құрылған.қпен сарғалдақ...
3 - Напишите сочинение на тему проблема человек и природа в рассказе липа воронин...
2 - Ы/-гі+келеді» формасын қолданып, сұрақтарға жауап жаз. 1) cен туған күніңе кімдерді...
2 - 10. как изменится среднее арифметическое пяти чисел, еслиодно из них уменьшить...
3 - Составить путешествие от стокгольма до севастополя и напишите страны через которые...
1