Используя 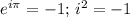 , доказать, что:
, доказать, что: 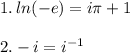
Другие вопросы по теме Алгебра
Популярные вопросы
- Какой степени числа 2 равно произведение: 1) 2 * 2 * 2;3) 2 * 2 * 2 *...
1 - 1. What comes to mind when you hear the word ‘family’? 2. How important...
2 - Выбери правильный вариант заполнения пропуска в предложении. Это светили…...
2 - Мәтінді мұқият оқыңыз. Тапсырмаларды орындаңыз. Внимательно прочитайте...
2 - match the words with their meanings: 1. Nematoda a) animals with hair...
3 - решить ее распишите это уравнение только Б...
1 - Ерлан создал собственную игру. Укажи вид программного обеспечения, с...
1 - Поместите контейнеры по порядку увеличения скорости испарения. Учитывайте,...
3 - Тапсырма 2. «Алып Ер Тұңға» жыры бойынша бос бағанды толтырыңыз. Жырдың...
2 - Подбери к данным вопросам соответствующий тип вопроса из списка Почему...
1
ln(-е)=ln|-е|+i*п=lnе+iп=1+iп
-i=-i^2/i=1/i=i^(-1)
Объяснение:
1.
lnz=ln|z|+iargz - главное значение логарифма
ln(-е)=ln|-е|+i*п=lnе+iп=1+iп
2.
домножим/разделим на i
-i=-i^2/i=1/i=i^(-1)