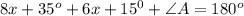Используя данные рисунка, найдите внутренние углы треугольника ABC.
Другие вопросы по теме Алгебра
Популярные вопросы
- Черты какого направления отразились в стихотворения ангел...
2 - Отношения а:в=10:5 найти обратное а)2,6б)0,26в)5:10г)2:3...
1 - төл жазу, ұлттық әліпби, негізделді, жетіл- діру, дыбыс, дыбысталуы,...
1 - пятый класс в учебнике этого нету...
1 - 1.There is no curriculum, grades, homework, testing or 2.Classes...
2 - ОЧЕНЬ НУЖНО! Задание на листке...
3 - Ардақты ат қастерлеу табиғаттың ерекше сыйы...
2 - 65В. Задай “толстые и тонкие вопросы по легенде. На тонкие вопросы...
1 - 1-тапсырма.Көмірсулар мен липидтердің құрылымын сипаттаңыз 2-тапсырма....
1 - Сколько километров пройдёт поезд за 10 часов Если за 2 часа 160...
1
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним
Сумма углов треугольника равна 180°
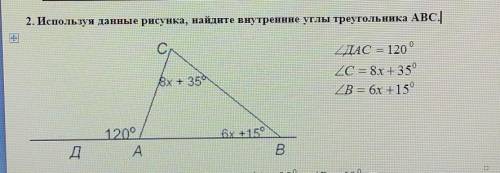
∠