1. Алгебра
  2. Игральную кость бросили один,

Игральную кость бросили один, два, три или четыре раза. Оказалось, что сумма всех выпавших очков равна 6. Какова вероятность того, что потребовалось сделать один бросок.

МарияМяуМяу МарияМяуМяу    2   06.01.2022 03:37    6

Ответы
аня2943 аня2943  16.02.2022 02:07

Пусть событие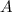 A - "выпало 6 очков", а событие 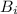B_i - "было произведено i бросков".

Предполагается, что количество бросков определяется случайно, то есть:

P(B_1)=P(B_2)=P(B_3)=P(B_4)=p=\dfrac{1}{4}

В данном случае конкретное числовое значение не столь важно, главное что оно одинаково для всех гипотез.

Для решения задачи понадобится формула Байеса:

P(B_1)\cdot P(A|B_1)=P(A)\cdot P(B_1|A)

Нам нужно найти вероятность того, что был 1 бросок, при условии того, что выпало 6 очков:

P(B_1|A)=\dfrac{P(B_1)\cdot P(A|B_1)}{P(A)}

Распишем полную вероятность:

P(B_1|A)=

=\dfrac{P(B_1)\cdot P(A|B_1)}{P(B_1)P(A|B_1)+P(B_2)P(A|B_2)+P(B_3)P(A|B_3)+P(B_4)P(A|B_4)}=

=\dfrac{p\cdot P(A|B_1)}{p\cdot P(A|B_1)+p\cdot P(A|B_2)+p\cdot P(A|B_3)+p\cdot P(A|B_4)}=

=\dfrac{P(A|B_1)}{P(A|B_1)+P(A|B_2)+P(A|B_3)+P(A|B_4)}

Найдем вероятности выпадения 6 очков при 1, 2, 3, 4 бросках.

При одном броске вероятность выпадения 6 очков, как и любого другого количества очков:

P(A|B_1)=\dfrac{1}{6}

При двух бросках, 6 очков может выпасть в следующих комбинациях:

{1; 5} - 2 вариант

(3; 3) - 1 вариант

{4; 2} - 2 вариант

Благоприятных вариантов - 5. Общее количество вариантов выпадения комбинации на двух кубиках равно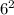 6^2.

P(A|B_2)=\dfrac{5}{6^2}

При трех бросках, 6 очков может выпасть в следующих комбинациях:

{1; 1; 4} - 3 варианта

(1; 2; 3) - 6 вариантов

Благоприятных вариантов - 9.Общее количество вариантов выпадения комбинации на трех кубиках равно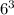 6^3.

P(A|B_3)=\dfrac{9}{6^3}

При четырех бросках, 6 очков может выпасть в следующих комбинациях:

{1; 1; 1; 3} - 4 варианта

(1; 1; 2; 2) - 6 вариантов

Благоприятных вариантов - 10.Общее количество вариантов выпадения комбинации на четырех кубиках равно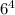 6^4.

P(A|B_4)=\dfrac{10}{6^4}

Таким образом, искомая вероятность:

P(B_1|A)=\dfrac{\dfrac{1}{6} }{\dfrac{1}{6}+\dfrac{5}{6^2}+\dfrac{9}{6^3}+\dfrac{10}{6^4}}=\dfrac{6^3}{6^3+5\cdot6^2+9\cdot6+10}=

=\dfrac{216}{216+180+54+10}=\dfrac{216}{460}=\dfrac{54}{115}

ответ: 54/115

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Юлиана95631 Юлиана95631  28.09.2019 11:30
1)сахарный песок при переработке теряет 2/15 своего веса. сколько надо взять сахарного песка , что бы получить 104 кг рафинада 2) в питомнике было 1800 саженцев . 25%...
Крейми51 Крейми51  28.09.2019 11:30
(12y-3(y-4))+9y докажите, что значение выражения не зависит от y...
reginochka33 reginochka33  28.09.2019 11:30
Построить график функции : y=x²-5x-3|x-2|+6...
Fjkskdnxk Fjkskdnxk  28.09.2019 11:30
Изобразите три прямые,пересекающиеся в одной точке на сколько частей они разбивают плоскость...
0blako 0blako  28.09.2019 11:30
9.2 (x/y)^8: (x^2/y)^4*xy^5 (xy^3)^7*(x^6y^4)^3: (x^24y^32) x^5y^8*(xy)^5: (x^5y^3)^2...
alina1923 alina1923  28.09.2019 11:30
Доказать что: сумма чисел 5m-3n и числа, противоположного числу m-7n, делится на 4,если m и n натуральные числа. мне нужно не только решение но и объяснение если можно)...
Dimka3113 Dimka3113  28.09.2019 11:30
9.2 (x/y)^8: (x^2/y)^4*xy^5 (xy^3)^7*(x^6y^4)^3: (x^24y^32) x^5y^8*(xy)^5: (x^5y^3)^2 30...
MashaBendyuk MashaBendyuk  28.09.2019 11:30
Запешите число в стандартном виде и укажите его порядок 1 ) 5 000 000 2)0,05 3) 0, 00064...
dashamaer2 dashamaer2  28.09.2019 11:30
30 . постройте график функции: 1)y=2+x в квадрате 2)y=2(x+3)в квадрате 3)y=-4(x-2) в квадрате...
знаниепуть знаниепуть  12.07.2019 11:30
Автомобилист увеличив скорость на 30 км\ч , за 5 ч преодолел путь на 90 км меньше чем предполагал проехать за 7ч .с какой скоростью двигался автомобилист?...

Популярные вопросы