H(x)=1+g(x) это функция четная или нечетная?
Другие вопросы по теме Алгебра
Популярные вопросы
- Написать текст рассуждение на тему какой предмет больше нравится? ( Биология...
3 - Прочитай пары предложений. Запиши только те предложения, в которых глаголы...
2 - Найдите расстояние от точки М до прямой АВ ...
1 - Fill in the gaps with can or ll will beable to....
2 - С першої грядки зібрали 18кг полуниці,с другої 22 Скільки зібрали полуниці...
2 - Составьте предложение по во Подчеркните главные члены. Укажите части речи,...
3 - Найдите значение алгебраической дроби если X=4, Y=3, ...
3 - Расчеты растягивающей силы между Солнцем и Марсом, если их массы составляют...
2 - Назовите самую маленькую и самую большую страну в каждом из регионов...
1 - Выбери формулы для линейных функций, графики которых изображены на схематичном...
2
Пусть функция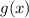 чётна. По определению это значит, что
чётна. По определению это значит, что 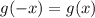 . Получим:
. Получим:
Это значит, что функция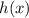 тоже чётна.
тоже чётна.
Теперь пусть функция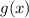 нечётна. По определению это значит, что
нечётна. По определению это значит, что 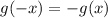 . Получим:
. Получим:
Это значит, что функция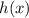 не является ни чётной, ни нечётной (за исключением случая, когда функция g(x) является нулевой константой).
не является ни чётной, ни нечётной (за исключением случая, когда функция g(x) является нулевой константой).
ответ: если g(x) чётна, то h(x) тоже чётна. Если g(x) нечётна, то h(x) не является ни чётной, ни нечётной (за исключением случая, когда g(x) является нулевой константой, — тогда h(x) является чётной).