(х-а) (4х-1) (х+в)>0 имеет решение (-∞;-3)∪(1/4;9) найдите значения а и в
Другие вопросы по теме Алгебра
Популярные вопросы
- Написать 3 предложение с однородным подчинением...
2 - 968: масса тыквы 2 кг 800 г. найдите массу: а) одну четвертую тыквы....
3 - Мне ! точки а и в лежат на окружности одного основания цилиндра, а...
3 - Реши уравнения. 39655+(x-52) = 69692 24000: x=48000: 80 50xa=1244x250...
2 - Решить уравнение 5: 7: 3/8=y: 28/75...
2 - Найдите сумму целых чисел на координатной оси, удалённых на 7 единиц...
3 - Составьте предложения 1. сущ. + прил. + числ. + гл. 2. гл + предл +...
2 - Перевести предложение на : по субботам или воскресеньям я обычно маме...
1 - Ознакомьтесь со структурой письменной характеристике. составьте характеристику...
1 - Слово из букв: д а о к р н слова из 4 букв. как можно больше!...
3
Нули выражения, записанного слева: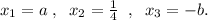
Решение неравенства имеет вид: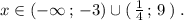
Знаки выражения, записанного слева, чередуются таким образом;
Поэтому в условии надо перед всей левой частью поставить знак минус, или записать неравенство со знаком меньше, а не больше.
То есть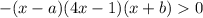 или
или 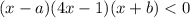 .
.
Тогда возможен вариант ответа: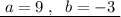 .
.
Вид неравенства: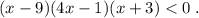
Либо неравенство можно было записать , например, так:
Но заданное неравенство не будет иметь тот ответ, что записан в условии . Наверное, произошла описка и неравенство было задано со знаком меньше, а не больше.