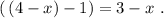Х^2 log 243 (4-x)<= log 3 (x-4)^2
Другие вопросы по теме Алгебра
Популярные вопросы
- 1)Фигура которого четыре прямых угла, фигура у которого два прямых...
3 - Морфологичный розбир слова чудові садочки...
1 - В какой четверти лежит угол,равный 172°=...
1 - №4З. В кролика чорна пігментація шерсті домінує над альбінізмом...
3 - Составить развернутый(сложный) план по § 2. история россии...
1 - Химия Напишите план приготовления раствора...
2 - Тортайдың арманы туралы.жауап берндерш...
3 - Обчисліть масові частки елементів: 1) у мурашиній кислоті HCOOH...
1 - Округлите число до десятков : 256032 ...
2 - Скок нужно денег чтобы закончить надо чтобы купит 10000голды?...
3
Используем метод рационализации, так как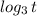 функция возрастающая , то знак
функция возрастающая , то знак 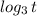 совпадает со знаком ( t-1 ) . Знак
совпадает со знаком ( t-1 ) . Знак 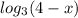 совпадает со знаком
совпадает со знаком