Группа туристов отправилась в 8ч утра на прогулку на моторной лодке по течению реки. отплыв от пристани на некоторое расстояние, туристы сделали на берегу привал на 2 ч и вернулись обратно в 16ч 15мин. на какое расстояние
отплыли туристы, если известно, что скорость лодки в стоячей воде равна 15км/ч, а скорость течения реки равна 3 км/ч? ps решить уравнением
Другие вопросы по теме Алгебра
Популярные вопросы
- Вкомнате темно. в ящике комода лежат 10 коричневых и 10 красных...
3 - Почему добро творить труднее чем зло? и почему маленькое добро...
3 - Найдите значение выражения (a+1/a+2)*1/a-1 если а=-5...
3 - Написать уравнение электролиза раствора содержащего смесь нитрата...
3 - Подбери подходяший по смислу предлог сделал бумаги вышел дома сверкает...
2 - Нужна ли здесь запятая после слова то ? несмотря на то что небо...
3 - Что является осью симметрий прямоугольника и ромба...
3 - По 9 класс. нужно! всем разложите на множители: 1. 1+cos b+cos...
3 - Какие поэты создали произведения о твоей родине...
2 - Укажи падеж имён прилагательных в пословицах: плохая шутка до добра...
1
Пусть х - искомое расстояние. Тогда до привала они плыли по течению -
- х/18 часов. Потом привал - 2 часа, потом обратно то же расстояние, но против течения - х/12 часов. Общее время: 16,25 - 8 = 8,25 часа.
Уравнение:
х/18 + 2 + х/12 = 8,25
Или х/18 + х/12 = 25/4
(5/36)*х = 225/36
х = 225/5 = 45 км.
ответ: 45 км.
15+3=18(км/ч) - скорость лодки по течению
15-3=12 (км/ч) - скорость лодки против течения
Пусть расстояние, на которое отплыли туристы, равно х км. Тогда по течению они плыли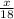 часов, а против течения
часов, а против течения 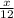 часов. Учитывая привал, который длился 2 часа, всего в пути туристы были 16,25 - 8 - 2 = 6,25 (часов). Составляем уравнение:
часов. Учитывая привал, который длился 2 часа, всего в пути туристы были 16,25 - 8 - 2 = 6,25 (часов). Составляем уравнение:
2х+3х=225
5х=225
х=45
ответ. 45 км.