1. Алгебра
  2. Гипербола 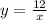пересекает окружность

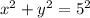Гипербола y=\frac{12}{x} пересекает окружность x^{2} +y^{2} = 5^{2} в точке А и В которые лежат в первой четверти. Найти скалярное произведение ОА*ОВ

ksenia07schapov ksenia07schapov    3   17.08.2020 14:08    1

Ответы
Kharin86 Kharin86  15.10.2020 16:05

Найдем координаты точек пересечения.

Составим и решим систему:

\begin{cases} y=\dfrac{12}{x} \\ x^2+y^2=5^2 \end{cases}

Подставим соотношение для у во второе уравнение:

x^2+\left(\dfrac{12}{x} \right)^2=25

x^2+\dfrac{144}{x^2} -25=0

Домножим на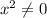 x^2\neq 0:

x^4-25x^2+144=0

Решим биквадратное уравнение:

D=(-25)^2-4\cdot1\cdot144=49

x^2=\dfrac{25+\sqrt{49} }{2} =16\Rightarrow x=\pm 4

x^2=\dfrac{25-\sqrt{49} }{2} =9\Rightarrow x=\pm 3

Так как точки А и В лежат в первой четверти, то их координаты положительные. Выберем положительные значения х и для них вычислим соответствующие значения у:

x=4\Rightarrow y=\dfrac{12}{4} =3

x=3\Rightarrow y=\dfrac{12}{3} =4

Получившиеся значения у положительны, значит точки лежат в первой четверти. Таким образом, координаты точек найдены.

Пусть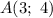 A(3;\ 4), B(4;\ 3).

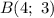Тогда, координаты векторов:

\vec{OA}=\{3;\ 4\}

\vec{OB}=\{4;\ 3\}

Скалярное произведение векторов равно сумме попарных произведений соответствующих координат:

\left(\vec{OA}\cdot\vec{OB}\right)=3\cdot4+4\cdot3=12+12=24

ответ: 24

ПОКАЗАТЬ ОТВЕТЫ
ekatsinrom ekatsinrom  15.10.2020 16:05

Объяснение:см. во вложении


Гипербола пересекает окружность в точке А и В которые лежат в первой четверти. Найти скалярное про
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
FizTex FizTex  22.11.2020 19:56
Решите задачу по алгебре! Известно, что Найдите...
GuldanaManarbek GuldanaManarbek  22.11.2020 19:56
Самостоятельная работа по теме преобразование буквенных выражений 7 класс 2 вариант +приложено...
лиод1 лиод1  22.11.2020 19:57
Многочлены слишком сложные...
Дани4ка14 Дани4ка14  22.11.2020 19:58
Найди число x (Не изменяй основание, данное в условии!)...
Star3111 Star3111  22.11.2020 19:58
Решите уравнение обозначив одну из взаимопропорциональных дробей через t,другую через 1\t...
калина007 калина007  13.08.2019 00:10
Мастер и ученик, работая вместе, заканчивают на час раньше, чем мастер, работая один, но на полчаса позже, чем мастер и два ученика. за какре время выполнят данное два...
larion266 larion266  13.08.2019 00:10
Сколько целых восьмизначных чисел можно записать тремя единицами и пятью нулями...
ярослававас ярослававас  23.12.2020 19:18
Скорость катера в стоячей воде равна x км/ч, а скорость течения реки равна 2 км/ч. Напиши скорость движения катера по течению....
infourazyukp092y0 infourazyukp092y0  23.12.2020 19:18
ученик определил среду предложенных растворов и записал наблюдение. По данным, определите среду и значение pH исследуемых растворов ​...
Стас666228 Стас666228  23.12.2020 19:19
Решите графическим методом систему уравнений {x+5=3 {y+2x=8​...

Популярные вопросы