Функция задана формулой f(x)=2x^2-11x. При каких xf(x)=6? Запишите ответы в порядке возрастания
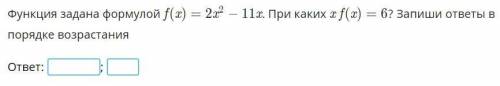
Ответы
Добрый день! Рад, что вы обратились ко мне для помощи. Давайте вместе решим задачу.
У нас дана функция f(x)=2x^2-11x и мы должны найти значения x, при которых f(x)=6.
Для начала, заменим f(x) в уравнении на 6:
6=2x^2-11x
Теперь приведем уравнение к квадратному виду:
2x^2-11x-6=0
Мы можем решить это квадратное уравнение, используя метод дискриминанта.
Для этого найдем дискриминант (D): D=b^2-4ac,
где a=2, b=-11, c=-6.
D=(-11)^2-4(2)(-6)
D=121+48
D=169
Так как D>0, у нас есть два различных корня.
Формула для нахождения корней квадратного уравнения: x=(-b±√D)/2a
Теперь найдем каждый из корней:
Корень 1: x=(-(-11)+√169)/2(2)
x=(11+13)/4
x=24/4
x=6
Корень 2: x=(-(-11)-√169)/2(2)
x=(11-13)/4
x=-2/4
x=-1/2
Таким образом, чтобы функция f(x) была равна 6, значения x должны быть равны 6 и -1/2.
Ответ: x=6, -1/2.
Надеюсь, что я понятно объяснил решение задачи. Если у вас есть еще вопросы, не стесняйтесь задавать!
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Популярные вопросы
- Якщо 1% від числа- 5, то це число...
3 - Найди значение выражения: (5,9−8):3,4 (ответ округли до десятых)....
3 - Заполни пропуски с рисунка...
3 - 1381. Стрех лугов собрали 19,7 т сена. С первого и второго лугов со- брали...
3 - Два задания по функциям. за лучший ответ...
1 - Переведите фразы, обращая внимание на союзы both… and, as… as, than, not...
1 - ⁸Встановіть відповідність між термінами та їх значенням. 1 «Метафізична...
2 - , даю всё, что есть, умоляю...
3 - 4. Літеру е треба писати в усіх словах рядка * р..ф..рендум, фа..тон, інт..лект...
3 - Заполните таблицу, определив недостающие массы раствора, воды, соли (растворенного...
2