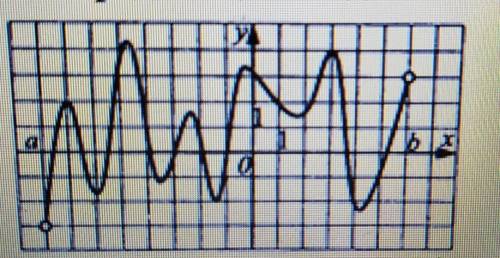
Функция у = f(x) определена на промежутке (a,b). На рисунке изображен график ее
производной. Укажите число а) точек
минимума:
б) промежутков убывания:
В) касательных проведенных к графику функции
под углом 30° к положительному направлению оси
ОХ.
Другие вопросы по теме Алгебра
Популярные вопросы
- Составьте и напишите фразу: иллюстрации и.я.бибилина к сказке о царе мне потому...
3 - Объем = 20 м\с кинетическая энергия 10 дж масса= ?...
2 - Почему екатерина 2 больше обращала внимание на дворянство...
2 - Вком л.н.толстой видит решающую силу в романе война и мир?...
1 - 4. укажите предложение, в котором сравнение выражаются сравнительным оборотом....
1 - Вес тела в воздухе 80 н определите вес этого тела в воде если на него действует...
1 - Порівняйте ступінь господарську освоєності людиною украйнського полісся та украйнського...
2 - Причины перехода к новой политике. основные направления нэпа. какие два урока...
3 - Моя любимая учительница по и сочинение повествование 15 предложений...
2 - Нужно сочинение 200 слов (1) всѐ чаще я с печальным вздохом в душе думаю о том,...
2
a) Точки минимума:
Точки минимума соответствуют тем моментам, когда значение производной меняется с отрицательного на положительное. В данном случае, на графике видны две такие точки, обозначенные как A и B.
b) Промежутки убывания:
Промежуток убывания соответствует тем отрезкам, где значение производной отрицательно. В данном случае, на графике видны два таких промежутка: от точки A до точки B и от точки C до точки D.
c) Касательные, проведенные к графику функции под углом 30° к положительному направлению оси ОХ:
Чтобы провести касательные под углом 30° к положительному направлению оси ОХ, мы должны найти точки на графике производной, где значение производной равно тангенсу 30°, который равен 1/√3 или около 0.577.
На графике можно увидеть две такие точки, обозначенные как E и F.
Затем, чтобы найти соответствующие точки на графике функции у = f(x), мы должны найти соответствующие значения x на оси абсцисс в точках E и F.
Таким образом, ответы на вопросы:
а) Точки минимума: A и B.
б) Промежутки убывания: [A, B] и [C, D].
в) Касательные, проведенные к графику функции под углом 30° к положительному направлению оси ОХ: точки E и F (соответствующие значения x на оси абсцисс необходимо уточнять).