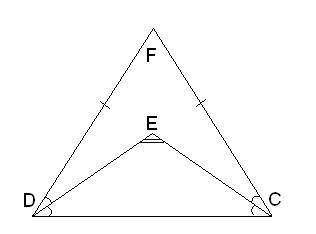
(фото прикреплено) DF=CF;DE− биссектриса∢FDC;CE− биссектриса∢FCD;∢DEC=154°.
Угол CFD равен ... °

Для решения данной задачи нам пригодятся свойства биссектрис треугольника и свойства углов при параллельных прямых.

Из условия задачи известно, что DF=CF и DE является биссектрисой ∢FDC, а CE - биссектрисой ∢FCD. Также дано, что ∢DEC = 154°.

Сначала найдем величину угла ∢CED. Поскольку DE является биссектрисой ∢FDC, она делит угол ∢FDC на два равных угла ∢CED и ∢DEB.

Так как DF равно CF, то треугольник DCF является равнобедренным треугольником. Это означает, что ∠DFC и ∠DCF равны. Так как ∠CED и ∠DCF являются смежными углами, то ∠CED также равен ∠DCF. Обозначим эту величину угла как "х".

Теперь воспользуемся свойством суммы углов в треугольнике. В треугольнике CED имеем:

∠CED + ∠CDE + ∠DEC = 180°.

Подставляем известные значения:

∠CED + ∠CDE + 154° = 180°.

∠CED + ∠CDE = 26°. (1)

Снова воспользуемся свойством равенства углов при параллельных прямых. Треугольник CFD может считаться подобным треугольнику CED в силу биссектрис.

Это означает, что ∠CFD также равен ∠CED, то есть "х".

Из равнобедренности треугольника DFC следует, что ∠DFC равен ∠DCF, то есть "х".

Так как сумма углов треугольника равна 180°, то:

∠CFD + ∠CDF + ∠DFC = 180°.

"х" + ∠CDF + "х" = 180°.

∠CDF + 2"х" = 180°.

∠CDF = 180° - 2"х". (2)

Теперь объединим (1) и (2):

∠CDF = 180° - 2"х" = 180° - 2(26°) = 180° - 52° = 128°.

Таким образом, угол CFD равен 128°.