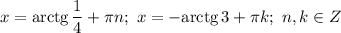Это какой-то капец... Решите и это Дедлайн до завтрашнего утра
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите программу(паскаль) нахождения суммы элементов массива а[1..15], кратных...
3 - Провідміняйте числівник пятсот девять...
1 - 1) в каком году численность населения в омской области была наибольшей? ответ:...
1 - Составить краткий пересказ параграфа по россии 6 класс тема: первые государства...
3 - Напишите стих со словами почки настаёт листочек поёт 33...
1 - Водном стручке 6 горошин. сколько горошины в 3таких стручках...
3 - Воробей, ворон, ворона, дятел, журавль, зимородок, клест, кукушка, куропатка,...
3 - Exercise 13. put the verb to be in the plural and change the sentence accordingly:...
3 - Окончание в слове тихую выражает значение единственного числа женского рода...
2 - Sinx+sin5x=корень из 2 sin3x решить, только подробно, ....
3
Так как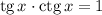 , то
, то 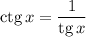
Сделаем соответствующую замену: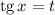
Обратная замена:
ответ: