1. Алгебра
  2. если лень решать, натолкните

если лень решать, натолкните хотя бы на мысль. ​


если лень решать, натолкните хотя бы на мысль. ​

LonelyOne LonelyOne    1   22.05.2021 00:58    0

Ответы
bolbatunovao bolbatunovao  21.06.2021 01:48

|\sqrt{16-x^2}+x|=12-2x. На ОДЗ (|x|\le 4| ) правая часть неотрицательна, поэтому уравнение равносильно совокупности

\left [ {{\sqrt{16-x^2}+x=12-2x} \atop {\sqrt{16-x^2}+x=2x-12}} \right.

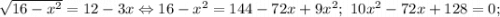
1) \sqrt{16-x^2}=12-3x\Leftrightarrow 16-x^2=144-72x+9x^2;\ 10x^2-72x+128=0;

(внимание! равносильность на ОДЗ - ведь при возведении в квадрат надо проверять неотрицательность правой части)

\left [ {{x=4} \atop {x=\frac{16}{5}}} \right.; оба лежат в ОДЗ.

2) \sqrt{16-x^2}=x-12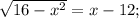; решений тут нет из-за отрицательности правой части на ОДЗ.

В ответ нужно написать упятеренную сумму корней; нам не жалко, можем  и упятерить, и сложить.

ответ: 36

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ГлебGleb39 ГлебGleb39  31.03.2022 07:49
очень надо. Привести уравнения кривых второго порядка к каноническому виду. Найти координаты фокусов, сделать чертеж. а) -=16 б) +-x-y-0,5=0 в) +=12...
zhdiana0706 zhdiana0706  31.03.2022 07:58
Упростите выражение: (а – b)(а + b) – (a^2 + 4b^2)...
kirillmich16 kirillmich16  31.03.2022 08:02
Яка функція є лінійною? а) у=21/х б) у=21-4/7х в) у=х^2-21 г) відсутня правильна відповідь ( если кому не понятно / это дробь, а ^ это степень )...
gona1 gona1  31.03.2022 08:02
Знайдіть суму десяти перших членів арифметичної прогресії, у якої перший член дорівнює 8, а десятим є число -22...
vadimsivun3 vadimsivun3  31.03.2022 08:28
Не даётся мне эта тема... Максимум , вычислить первые 5 членов последовательности, которая задана формулой n-го члена (дробь): an = (21 - n^2)/2...
tatgomer tatgomer  31.03.2022 08:34
У шафі 24 книги з них 6 посібники скільки відсотків книг становлять посібники?...
NastyaMeow05 NastyaMeow05  31.03.2022 08:37
очень надо. Даны точки А, В, С, D. Найти: а) площадь треугольника АВС; б) объем пирамиды ABCD; в) уравнение плоскости, проходящей через точку D параллельно плоскости АВС;...
ukaldarbek206 ukaldarbek206  31.03.2022 08:40
Побудуйте графік функції у = -2х-2. Вкажіть значення х, яке є нулем функції. Для яких значень х функцiя набуває вiд ємних значень?...
firudinnerimano firudinnerimano  31.03.2022 08:47
Скількі двоцифрових чисел можна скласти з чисел 0 4 5...
Викитирон Викитирон  17.03.2019 12:20
Нужно сделать : есть число шестая часть которого меньше его половины на 1.5....

Популярные вопросы