1. Алгебра
  2. если лень решать, натолкните

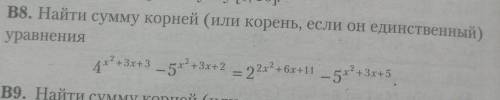
если лень решать, натолкните хотя бы на мысль ​


если лень решать, натолкните хотя бы на мысль ​

leski leski    1   14.05.2021 22:43    0

Ответы
ТупицаТян ТупицаТян  13.06.2021 22:44

-3

Объяснение:

4^{x^{2}+3x+3}-5^{x^{2}+3x+2}=2^{2x^{2}+6x+11}-5^{x^{2}+3x+5};

(2^{2})^{x^{2}+3x+3}-2^{2x^{2}+6x+11}=5^{x^{2}+3x+2}-5^{x^{2}+3x+5};

2^{2x^{2}+6x+6}-2^{2x^{2}+6x+11}=5^{x^{2}+3x+2} \cdot (1-5^{3});

2^{2x^{2}+6x+6} \cdot (1-2^{5})=5^{x^{2}+3x+2} \cdot (1-125);

2^{2x^{2}+6x+6} \cdot (1-32)=5^{x^{2}+3x+2} \cdot (-124);

2^{2x^{2}+6x+6} \cdot (-31)=5^{x^{2}+3x+2} \cdot (-124) \quad | :(-124)

\dfrac{2^{2x^{2}+6x+6}}{4}=5^{x^{2}+3x+2};

\dfrac{2^{2x^{2}+6x+6}}{2^{2}}=5^{x^{2}+3x+2};

2^{2x^{2}+6x+6-2}=5^{x^{2}+3x+2};

2^{2x^{2}+6x+4}=5^{x^{2}+3x+2};

(2^{2})^{x^{2}+3x+2}=5^{x^{2}+3x+2};

4^{x^{2}+3x+2}=5^{x^{2}+3x+2};

\dfrac{4^{x^{2}+3x+2}}{5^{x^{2}+3x+2}}=1;

\bigg (\dfrac{4}{5} \bigg )^{x^{2}+3x+2}=1;

x^{2}+3x+2=0;

Согласно теореме Виета, сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком:

x_{1}+x_{2}=\mathbf {-3};

ПОКАЗАТЬ ОТВЕТЫ
ІванДурненький ІванДурненький  13.06.2021 22:44

4^(x^2 + 3x + 3) - 5^(x^2 + 3x + 2) = 2^(2x^2 + 6x + 11) - 5^(x^2 + 3x + 5)

4^(x^2 + 3x + 3) - 5^(x^2 + 3x + 2) = 2^(2(x^2 + 3x + 3) + 5) - 5^(x^2 + 3x + 2 + 3)

4^(x^2 + 3x + 3) - 5^(x^2 + 3x + 2) = 32*2^(x^2 + 3x + 3) - 125*5^(x^2 + 3x + 2)

124*5^(x^2 + 3x + 2) = 31*4^(x^2 + 3x +2 + 1)

124*5^(x^2 + 3x + 2) = 31*4*4^(x^2 + 3x +2)

124*5^(x^2 + 3x + 2) = 124*4^(x^2 + 3x +2)

5^(x^2 + 3x + 2) = 4^(x^2 + 3x +2)

(5/4)^(x^2 + 3x + 2) = 1

x^2 + 3x + 2 = 0

D = 9 - 4*2 = 1

x₁₂ = (-3 +- 1)/2 = -1   -2

x₁ = -1

x₂ = -2

x₁ + x₂ = -1 - 2 = -3

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
kalinkamalinka369 kalinkamalinka369  19.03.2019 07:50
Решить уравнение x3 – 4x2 – 9x + 36 = 0...
danasveshnikova danasveshnikova  19.03.2019 07:07
Решить неравенство! , ! 2^(x)+2^1-x) 3...
SemenOr SemenOr  19.03.2019 07:08
Ввершинах квадрата расставлены натуральные числа. известно, что из двух чисел, стоящих концах любой стороны, одно делится на другое, а из двух чисел, стоящих в концах любой диагонали...
Лина5678 Лина5678  19.03.2019 07:50
Вкуске было 96 м ткани.для дет сада взяли 3/8 этого куска,а для дет. яслей 5/12 этого куска. сколько материи ещё осталось в куске?...
Кентервильский1монах Кентервильский1монах  19.03.2019 07:40
Cos 7x cos 3 x - sin 3 x sin 7 x - 1\2...
Tiktak222 Tiktak222  19.03.2019 07:40
Вравнобедренном треугольнике abc с основанием ac длина боковой стороны равна 20.найдите косинус угла bac если высота проведенная к основанию равна 12...
BelkaNext BelkaNext  19.03.2019 07:40
8! кто может ! вынесите множитель из-под знака корня. кводратный корень- к(так как значок я ствить не умею, заменяю буквой) /-дробь а теперь сами числа: к m(в третий степени)/n(в...
юра416 юра416  19.03.2019 07:40
Найдите общий множитель: 8х^6y^3-12x^3y^3...
alyakolomoets alyakolomoets  19.03.2019 07:40
16*(9 в степени х)-25*(12 в степени х)+9*(16 в степени х)=0...
ггвв ггвв  19.03.2019 07:40
X- 4/x - 2корня из x сократите дробь...

Популярные вопросы