Если количество положительных четных делителей 337500 равно N, а количество положительных нечетных делителей равно M, то N-M =? варианты:
А 28
B 48
C 24
D 11
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите и исправьте ошибку (ошибки) в образовании формы слова (слов). Запишите правильный...
1 - Воспользуйтесь теоремой косинусов и найдите угол между векторами:...
2 - На швейной фабрике изготовляют кожаные мячи радиусом 20 см. Сколько квадратных метров...
2 - 4. Какие географические факторы различиям между Вос точной, Центральной и Западной...
2 - Известно что график функции проходит через точку (k;2)...
2 - Дано: вектора a⃗⃗ (3x-4; -7) и b⃗⃗ (20; 6-y) которые равны. Найти x и y....
2 - 1. Задача. Ввести массив состоящий из 5 элементов. (Python) 2. Задача. Вывести массив...
2 - Сила тока в цепи электрической лампы равна 0,3 А. Сколько электронов проходит через...
3 - ПОЖ Что не является СПС? 1) Закон 2) Консультант+ 3) Гарант 4) Референт 5) Кодекс...
3 - ВОПРОСЫ И ЗАДАНИЯ 1. Что такое аудиоинформация? 2. Что такое видеоинформация? 3....
3
Четный делитель рассматриваемого числа имеет вид , где
, где  и
и  нечетно, причем ясно, что
нечетно, причем ясно, что  -- нечетный делитель числа. Сопоставим каждому нечетному делителю
-- нечетный делитель числа. Сопоставим каждому нечетному делителю  какое-нибудь число
какое-нибудь число 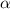 . Тогда пусть
. Тогда пусть 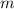 -- максимальная степень двойки, которая делит
-- максимальная степень двойки, которая делит  , а
, а  -- все нечетные делители числа
-- все нечетные делители числа  . В таком случае
. В таком случае  -- все четные делители числа
-- все четные делители числа  . Нетрудно видеть, что их в точности
. Нетрудно видеть, что их в точности  . Получается
. Получается  . Эта величина, очевидно, равна количеству делителей числа
. Эта величина, очевидно, равна количеству делителей числа 