1. Алгебра
  2. Если двузначное число

Если двузначное число разделить на сумму его цифр, то в частном получится 8, а в остатке 7. Если же разделить это число на разность его цифр, то в частном получится 11, а в остатке 5. Найди это число !

irochkakarpenkp0bint irochkakarpenkp0bint    2   14.01.2022 18:53    3

Ответы
Lerochka0204 Lerochka0204  14.01.2022 19:00

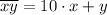
Двузначное число \overline{xy}=10\cdot x+y

Если двузначное число разделить на сумму его цифр, то в частном получится 8, а в остатке 7

10\cdot x+y=8(x+y)+7

Если же разделить это число на разность его цифр, то в частном получится 11, а в остатке 5.

10\cdot x+y=11(x-y)+5

Решаем систему уравнений:

\left \{ {{10\cdot x+y=8(x+y)+7} \atop {10\cdot x+y=11(x-y)+5}} \right.   \Rightarrow \left \{ {{10x+y=8x+8y+7} \atop {10x+y=11x-11y+5}} \right. \Rightarrow \left \{ {{2x-7y-7=0} \atop {x-12y+5=0}} \right.

Умножаем второе уравнение на (-2)

\left \{ {{2x-7y-7=0} \atop {-2x+24y-10=0}} \right.

Складываем (вместо первого уравнения - сумма ; вместо второго  - любое, в том числе и те,  которые были первоначально)

\left \{ {{17y-17=0} \atop {x-12y+5=0}} \right.

\left \{ {{y=1} \atop {x-12+5=0}} \right.

\left \{ {{y=1} \atop {x=7}} \right.

О т в е т. 71

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ZEWER ZEWER  30.04.2021 13:33
Решите уравнение и выполните проверку по теореме,обратной теореме Виета: а) х²-5√2х+12=0б) х²+2√3х-72=0 ​...
Sino4ka Sino4ka  30.04.2021 13:33
1.Знайдіть критичні точки функції 1)у=4х^3-5х^2-х....
sohibjon457 sohibjon457  30.04.2021 13:34
Розв яжіть дробове раціональне рівняння6x-10/x²=3x-2x²/4x²​...
zexer9p07xi1 zexer9p07xi1  01.09.2019 23:10
Найдите корень уравнения 2х2-y-1=х2--х2) над 2 и х - это степени....
rdemchenko rdemchenko  01.09.2019 23:10
Найти значение выражения: 26sin^2x, если sin x= -2/√13...
olyascochilyas olyascochilyas  01.09.2019 23:10
Найдите второй член арифметической прогрессии, в которой a5=10, d=-6....
komarrik komarrik  01.09.2019 23:10
Варифметической прогрессии выполняется зависимость a5-a4=4, a5+a4=12. найдите сумму первых десяти членов этой прогрессии....
Дария008 Дария008  01.09.2019 23:10
Для прогрессии: 16; 4; 1; 1/4; запишите формулу n-го члена....
namdokp09srw namdokp09srw  01.09.2019 23:10
За 4 коробки сока и 2 шоколадкм заплатили 220 р., а за такие же 2 коробки сока и 3 шоколадки заплатили 170 р.сколько стоит одна коробка сока и одна шоколадка?...
Xkdidid Xkdidid  01.09.2019 23:10
Пятый член прогрессии равен 54, а знаменатель равен 1,5. найдите сумму первых шести членов этой прогрессии....

Популярные вопросы