1. Алгебра
  2. Две бригады,работая вместе,выполнили

Две бригады,работая вместе,выполнили работу за 12 дней.сколько дней потребовалось бы каждой бригаде на выполнение этой работы,если одной из них на это требуется на 10 дней меньше,чем другой?

dvika12 dvika12    2   11.06.2019 17:40    5

Ответы
sweetmayers sweetmayers  09.07.2020 15:39

Примем всю работу за целое (1), тогда производительность обеих бригад  равна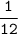 \tt\displaystyle\frac{1}{12}.

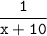Производительность первой бригады \tt\displaystyle\frac{1}{x}, а второй \tt\displaystyle\frac{1}{x+10}.

Составим уравнение:

\tt\displaystyle\frac{1}{x}+\frac{1}{x+10}=\frac{1}{12}   х≠0;  х≠ -10

12(x+10)+12x=x(x+10)

12x+120+12x=x^{2}+10x

-x^{2}+14x+120=0      |  *(-1)

x^{2}-14x-120=0

D=(-14)^{2}-4*1*(-120)=676

x_{1}=\tt\displaystyle\frac{-(-14)+\sqrt{676} }{2*1}=20 дней - потребуется первой бригаде

x_{2}=\tt\displaystyle\frac{-(-14)-\sqrt{676} }{2*1}=-6 - не подходит под условие

20+10=30 дней - потребуется другой бригаде

ответ: 20 и 30 дней.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Андрій008695652945 Андрій008695652945  23.10.2019 14:54
Уменя слишком маленький тезаурус, чтобы решить это вашей ! ​...
alena1706 alena1706  23.10.2019 14:54
Для нумерації сторінок в підручнику використали 2019 цифр, скільки сторінок в підручнику?...
ДжонниМультяшка ДжонниМультяшка  23.10.2019 14:51
запишите выражение 169[tex]x^{4} y^{8}[/tex] в виде степени...
katesgo katesgo  23.10.2019 14:48
По мо ги те ! возведите в степень произведение: [tex]( - 2a^{5} b^{4} )^{5}[/tex]...
mrsexobeat308 mrsexobeat308  23.10.2019 14:47
Найдите периметр фигуры. ответ запиши в виде многочлена стандартного вида и укажите его степень...
Гогенцоллерн Гогенцоллерн  23.10.2019 14:46
Решить , по человечески все в закрепе​...
По5643 По5643  23.10.2019 14:43
запишите в виде степени: [tex]\frac{(m3)^{2} * m^{4} }{m^{7} }[/tex]...
Motia2k17 Motia2k17  23.10.2019 14:42
Решить методом интервалов неравенство также на чертить отрезок n 72 номера 1) 2) 3)​...
Altama Altama  04.12.2020 11:43
Начертите график функции y=2x - 3 и y= -x + 3, укажите точку пересечения.​...
dimadi1 dimadi1  04.12.2020 11:43
2. Найдите координаты точек пересечения графиков функции:y =-6х+1 и у=5х+9​...

Популярные вопросы