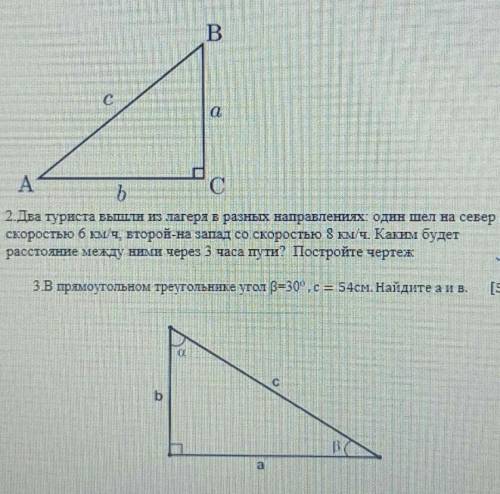
два туриста вышли из лагеря в разных направлениях Один шёл по север со скоростью 6 км в ч 2 на запад со скоростью 8 км ч С каким будет расстояние между ними 3 часа пути Попробуйте чертёж и второе задание в прямоугольном треугольнике угол B=30, c=54см найдите а и в

Для решения первой задачи о расстоянии между двумя туристами, которые движутся в разных направлениях, нам понадобятся знания о том, как вычислять расстояние по пройденному пути сочетанием движений в разных направлениях.

Первый турист идет по северу со скоростью 6 км/ч. За 3 часа он пройдет расстояние 6 км/ч * 3 ч = 18 км.

Второй турист идет на запад со скоростью 8 км/ч. За 3 часа он пройдет расстояние 8 км/ч * 3 ч = 24 км.

Теперь нужно определить расстояние между ними. Мы можем рассмотреть эту ситуацию как прямоугольный треугольник, где пройденные пути первого и второго туристов являются катетами, а расстояние между ними - гипотенузой. Для вычисления расстояния между ними, мы можем использовать теорему Пифагора.

Зная длины катетов 18 км и 24 км, мы можем найти гипотенузу (расстояние между туристами) по следующей формуле:
гипотенуза^2 = катет1^2 + катет2^2

Расстояние между туристами будет:
расстояние между туристами = sqrt(18^2 + 24^2)
расстояние между туристами = sqrt(324 + 576)
расстояние между туристами = sqrt(900)
расстояние между туристами = 30 км

Таким образом, расстояние между туристами через 3 часа пути будет 30 км.

Для решения второй задачи о прямоугольном треугольнике, где известны угол B и сторона c, нам понадобятся знания о тригонометрии.

Угол B равен 30 градусам, а сторона c равна 54 см. Мы хотим найти сторону а и сторону в.

У нас есть два способа решения этой задачи: использование тригонометрического отношения синуса или косинуса.

1. Использование синуса:
Мы знаем, что sin(B) = противолежащая сторона / гипотенуза.
Заменив значения, получим sin(30) = a / 54.
sin(30) = 1/2 (по формуле или таблице значений синуса угла 30).
Теперь мы можем выразить a: a = sin(30) * 54.
a = (1/2) * 54.
a = 27 см.

2. Использование косинуса:
Мы знаем, что cos(B) = прилежащая сторона / гипотенуза.
Заменив значения, получим cos(30) = a / 54.
cos(30) = sqrt(3)/2 (по формуле или таблице значений косинуса угла 30).
Теперь мы можем выразить a: a = cos(30) * 54.
a = (sqrt(3)/2) * 54.
a = 27*sqrt(3) см.

Таким образом, сторона а равна 27 см или 27*sqrt(3) см, в зависимости от выбранного способа решения.