1. Алгебра
  2. Два крана наполняют бассейн

Два крана наполняют бассейн за 2 часа. Если первый кран открыт в течение 2 часов, а второй кран - в течение 1 часа, 5/6 бассейна будет заполнено. Как долго каждый кран будет наполнять бассейн ПОЛНЫЙ ОТВЕТ С УРАВНЕНИЕМ ​


Два крана наполняют бассейн за 2 часа. Если первый кран открыт в течение 2 часов, а второй кран - в

Лееееешаааа Лееееешаааа    1   16.10.2020 14:53    1

Ответы
kycokbatona kycokbatona  15.11.2020 14:55

1 кран -4часа

2 кран-6часа

ПОКАЗАТЬ ОТВЕТЫ
YummyGirl YummyGirl  15.11.2020 14:55

Пусть за  x  час 1-й кран будет наполнять весь бассейн

за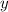    y  час 2-й кран будет наполнять бассейн.

Если 1 - это объем всего бассейна, тогда

\frac{1}{x}  - объем воды, который проходит через 1-й кран за 1 час.

\frac{1}{y}  - объем воды, который проходит через 2-й кран за 1 час.

(\frac{1}{x}+\frac{1}{y})  - общая производительность двух кранов.

\frac{1}{x}+\frac{1}{y}=\frac{1}{2}   - первое уравнение

2*\frac{1}{x}+1* \frac{1}{y}=\frac{5}{6}     - второе уравнение

Из первого уравнения получим: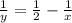 \frac{1}{y} =\frac{1}{2} -\frac{1}{x}  и вставим во второе уравнение:

2*\frac{1}{x}+ \frac{1}{2}-\frac{1}{x} =\frac{5}{6}

                  \frac{1}{x}=\frac{5}{6}-\frac{1}{2}

                  \frac{1}{x}=\frac{5}{6}-\frac{3}{6}=\frac{2}{6}=\frac{1}{3}

                  \frac{1}{x}=\frac{1}{3}

                  x=3

Подставим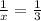    \frac{1}{x}=\frac{1}{3}  в первое уравнение:

                 \frac{1}{3}+\frac{1}{y}=\frac{1}{2}

                 \frac{1}{y}=\frac{1}{2}-\frac{1}{3}

                \frac{1}{y}=\frac{3}{6}-\frac{2}{6}=\frac{1}{6}

                \frac{1}{y}=\frac{1}{6}

                y=6  

ответ:  за 3 часа 1-й кран наполнит весь бассейн;

            за 6 часов 2-й кран наполнит весь бассейн.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
serpgo1 serpgo1  18.05.2020 16:57
При каких значениях переменных значение выражения -4х+5+у^2-2х+х^2 равно нулю? 8 класс 2 часа решаю, никак не получается...
Артём0Болдырев Артём0Болдырев  18.05.2020 16:57
Отметьте функции, которые являются прямой пропорциональностью. Выберите несколько из 4 вариантов ответа: 1) y=-3x^2 2) y=x/5 (это дробь) 3) y=x 4) y=x-7...
Colere Colere  18.05.2020 16:57
Сократить алгебраическую дробь 4⋅a^10/6⋅a^2 Выбери, в каком виде должен быть записан ответ, если c — положительное число: ° AB⋅ac ° A⋅acB Введи числитель A= Знаменатель B= Показатель...
koalakoalakoala koalakoalakoala  18.05.2020 16:57
Найдите значения х при которых функция не определена 9-4,5х/х^2-6x+9...
Никита11111114957558 Никита11111114957558  18.05.2020 16:57
Розвя жіть систему рівнянь...
Пусик95 Пусик95  09.08.2019 02:50
Моторная лодка милда плывёт по течению 12 км/ч марис плыл 2 часа по потоку...
milanaberezova milanaberezova  09.08.2019 02:50
Найдите корень уравнения: 13-3х=16+2х...
slavioglokolea77 slavioglokolea77  09.08.2019 02:50
Ира и мама собрали всего 36 бел. грибов, причём ира нашла на 40% больше бел. грибов чем мама. сколько грибов собрала ира?...
alexbarbos75 alexbarbos75  27.07.2019 21:00
Решите : группа школьников выехала на экскурсию из города а в город в на автобусе , а вернулась в город а по железной дороге , затратив на обратный путь на 30 минут больше , чем на...
КамиллаОк КамиллаОк  27.07.2019 21:00
Два тела , движущейся в одну сторону по окружности с постоянными скоростями , встречаются каждые 112 мин. при движении в противоположеные стороны - через каждые 16 мин. во втором случае...

Популярные вопросы