1. Алгебра
  2. Два экскаватора, работая вместе,

Два экскаватора, работая вместе, могут выкопать котлован за 12 дней.первый, работая отдельно, может выкопать этот котлован на 10 дней быстрее,чем второй.за сколько дней выкопает котлован каждый экскаватор, работая отдельно. с
системы уравнений.

aylinafedorovaoyhkfx aylinafedorovaoyhkfx    1   03.03.2019 23:20    5

Ответы
bydarinav2 bydarinav2  24.05.2020 00:46
Предположим, что второй экскаватор может вырыть котлован за х дней, тогда первый экскаватор может вырыть котлован за (х-10) дней

таким образом

\frac{1}{x-10} - производительность первого экскаватора

 

\frac{1}{x} - производительность второго экскаватора

 

(\frac{1}{x-10}+\frac{1}{x}) - производительность двух экскаваторов при их совместной работе, а из условия задачи их производительность равна \frac{1}{12}

согласно этим данным составим и решим уравнение:

 

\frac{1}{x-10}+\frac{1}{x}=\frac{1}{12}

 

12x+12(x-10)=x(x-10)

 

12x+12x-120=x^{2}-10x

 

24x-120=x^{2}-10x

 

x^{2}-10x-24x+120=0

 

x^{2}-34x+120=0

 

Cчитаем дискриминант:

 

D=b^{2}-4ac=(-34)^{2}-4\cdot1\cdot120=1156-480=676

 

Дискриминант положительный

 

\sqrt{D}=26

 

Уравнение имеет два различных корня:

 

x_{1}=\frac{-b+\sqrt{D}}{2a}=\frac{34+26}{2\cdot1}=\frac{60}{2}=30

 

x_{2}=\frac{-b-\sqrt{D}}{2a}=\frac{34-26}{2\cdot1}=\frac{8}{2}=4

 

не подходит по смыслу или не удовлетворяет условию, так как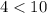 4<10

 

следовательно

х=30 (дней) - выкопает котлован второй экскаватор.

х-10=30-10=20 (дней) - выкопает котлован  первый экскаватор Предположим, что х - время одиночной работы первого экскаватора, у - время одиночной работы второго экскаватора

таким образом

\frac{1}{x} - производительность первого экскаватора

 

\frac{1}{y} - производительность второго экскаватора

 

согласно этим данным составим систему уравнений и решим её:

 

\left \{{{y=x+10}\atop{\frac{1}{x}+\frac{1}{y}=\frac{1}{12}}}\right

 

\frac{1}{x}+\frac{1}{x+10}=\frac{1}{12}

 

12(x+10)+12x=x(x-10)

 

12x+120+12x=x^{2}+10x

 

24x+120=x^{2}+10x

 

x^{2}+10x-24x-120=0

 

x^{2}-14x-120=0

 

Cчитаем дискриминант:

 

D=b^{2}-4ac=(-14)^{2}-4\cdot1\cdot(-120)=196+480=676

 

Дискриминант положительный

 

\sqrt{D}=26

 

Уравнение имеет два различных корня:

 

x_{1}=\frac{-b+\sqrt{D}}{2a}=\frac{14+26}{2\cdot1}=\frac{40}{2}=20

 

x_{2}=\frac{-b-\sqrt{D}}{2a}=\frac{14-26}{2\cdot1}=\frac{-12}{2}=-6

 

не удовлетворяет условию, так как отрицательные дни быть не могут

 

следовательно

х=20 (дней) - выкопает котлован  первый экскаватор.

y=x+10=20+10=30 (дней) - выкопает котлован второй экскаватор.

 

ответ: первый экскаватор выкопает котлован за 20 дней; второй экскаватор выкопает котлован за 30 дней.

 

ПОКАЗАТЬ ОТВЕТЫ
sokoldam4 sokoldam4  24.05.2020 00:46

пусть Х-дней работает один 1-й, тогда (Х+10)дней работает один 2-й.

значит 1/х - это скорость работы в день 1-го, а 1/(х+10) - скорость работы 2-го. вместе они работали 12 дней, следовательно получаем уравнение

12/х +12/(х+10) = 1  привидем  к общему знаменателю х(х+10) и оставим одни числители:

12х+12(х+10)=х(х+10)

12х+12х+120=х^2+10x

x^2-14x-120=0

D=676

x1=-6 - это отрицательное значение , чего быть не может при нашем условии

x2=20 -дней работал 1-й, 20+10=30-дней работаль 2-й.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
malika0408 malika0408  13.08.2019 11:50
80 за два дня велосипедист проехал s км. в первый день он проехал 2y км, а во второй-на 3 км меньше. составьте формулу зависимости s от y. вычислите расстояние, которое...
artemazarenko artemazarenko  13.08.2019 11:50
Нужно решить неравенство 2cos x-1 ≥0...
sveta7up sveta7up  13.08.2019 11:50
Прямоугольный треугольник с катетами 3и4 см в первый раз вращается вокруг меньшего катета ,а во второй раз вокруг большего катета . сравнить объемы этих конусов...
kasa0303 kasa0303  13.08.2019 11:50
На рисунке показано что из городов а и б расстояние между которыми равно 30 километров одновременно навстречу друг другу выехали две машины скорость первой машины 70 километров...
jenja117 jenja117  04.08.2019 08:30
Выражение: б)(2p+1,-p) г)b-(4-2b)+(3b-1)...
kokokola20 kokokola20  04.08.2019 08:20
Найти область определения функции 3х(х+5)...
vadim1154 vadim1154  04.08.2019 08:20
9a-b 3a-a^0,5*b^0,5 (числитель и знаменатель)...
nlimel nlimel  04.08.2019 08:20
Из пункта а в пункт б , расстояние между которыми равно 32 км, вышел пешеход со скоростью 5км/ч. через 10 минут из пункта б в пункт а выехал велосипедист со скоростью 12...
kskkksjsjsj kskkksjsjsj  04.08.2019 08:20
Найдите угол,смежный с углом abc,если 1)угол abc=36* 2)угол abc=102*...
nataly54 nataly54  02.03.2021 10:44
Известно что при некотором значении x значение выражения x^5x-1 равно 9. Найдите чему равно при этом же значении х значение следующего выражения: а)3x^2-15x-3b)x^2(x^2-5x-1)-5x(x^2-5x-1)c)9x^2-45x-7^-...

Популярные вопросы