дві бригади працюючи разом віконують деяку роботу за 2 дні. За скільки днів цю роботу виконала б кожна бригада окремо, якщо перщій бригаді на це потрібно на 3 дні більше, ніж другій?

Две бригады, работая вместе выполняют некоторую работу за 2 дня. За сколько дней эту работу выполнила бы каждая бригада в отдельности, если первой бригаде на это нужно на 3 дня больше, чем второй?

Решение.

Пусть за дней всю работу выполнила бы первая бригада, тогда

за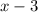     дней всю эту работу выполнила бы вторая бригада.

Примем весь объём работы за 1 (единицу), тогда

 -  производительность первой бригады;

  -  производительность первой бригады.

 -  общая производительность двух бригад.

Уравнение:

       (

             не удовлетворяет условию, т.к.

           удовлетворяет условию.

За 6 дней всю работу выполнила бы первая бригада.

За  6-3=3  дня всю эту работу выполнила бы вторая бригада.

ответ: 6 дней; 3 дня.