Довести, що при всіх допустимих значеннях змінної значення виразу не залежить від значення змінної, яка входить в нього

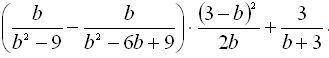
Довести, що при всіх допустимих значеннях змінної значення виразу не залежить від значення змінної,

Ответы

SofiaQueen 29.06.2021 00:15

Відповідь:

Пояснення:

Зделаем действия в скобках

b/(b^2-9) - b/(b^2-6b+3)= b/(b-3) ×(1/(b+3)-1/(b-3))= b/(b-3)× ((b-3-b-3)/((b+3)(b-3))=b/(b-3)×(-6)/((b+3)(b-3))

Умножение

(b/(b^2-9) - b/(b^2-6b+3))×(3-b)^2/2b=b/(b-3)×(-6)/((b+3)(3-b))×(3-b)^2/2b= -3/(b+3)

-3/(b+3) +3/(b+3)=0

ПОКАЗАТЬ ОТВЕТЫ

Ginjfthvgg 29.06.2021 00:15

$\Big(\dfrac{b}{b^2-9}-\dfrac{b}{b^2-6b+9}\Big)\cdot \dfrac{(3-b)^2}{2b}+\dfrac{3}{b+3}=\\\\\\=\Big(\dfrac{b}{(b-3)(b+3)}-\dfrac{b}{(b-3)^2}\Big)\cdot \dfrac{(3-b)^2}{2b}+\dfrac{3}{b+3}=\qquad \Big[\ b\ne 0\ ,\ b\ne \pm 3\ \Big]\\\\\\=\dfrac{b(b-3)-b(b+3)}{(b-3)^2(b+3)}\cdot \dfrac{(b-3)^2}{2b}+\dfrac{3}{b+3}=\\\\\\=\dfrac{b^2-3b-b^2-3b}{(b+3)\cdot 2b}+\dfrac{3}{b+3}=\dfrac{-6b}{(b+3)\cdot 2b}+\dfrac{3}{b+3}=\dfrac{-3}{b+3}+\dfrac{3}{b+3}=0$

В ответе получили число 0, а число не зависит от переменной. Поэтому значение выражения не зависит от значения переменной "b" , которая входит в него . Какое бы значение переменной "b" из области определения мы ни придавали, всё равно в ответе получим 0 .

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра