Доведіть що функція є непарною (x^3+2x)/(x^2-1)
Другие вопросы по теме Алгебра
Популярные вопросы
- Длина машины равна 3,97 м. Какова приблизительная длина автобуса? ответ запиши...
3 - 3. Склади хімічні реакції, за до яких можна здійснити такі перетворення. Н2О2-...
2 - проведите произольную прямую а С линейки и угольника постройте три прямые праллельные...
1 - Некоторое количество идеального газа нагревается при постоянном давлении. Во...
1 - ЗАДАНИЕ №4 ВРЕМЯ НА ВЫПОЛНЕНИЕ:12:31ТЕКСТ ЗАДАНИЯРаз был он в особенно хорошем...
1 - за правильное решение, все за ранее! Знайти невідому сторону трикутника ABC і...
2 - Read these sentences and fill in the gaps with the correct variant (must, mustn’t,...
2 - Напишите сочинение по плану. И. И. Левитан. Весна. Большая вода. 1. Вступление...
2 - Температура повітря на вершині гори дорівнює -4°С, а біля її підніжжя на висоті...
2 - Как называется песня, ага BLa ага вай вы чего, обасали гуся а потом фино, аоаоаоао...
2
Функція за означенням є непарною, коли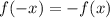 . Підставимо в нашу функцію
. Підставимо в нашу функцію 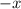 замість
замість 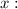
що і треба було довести.