, Доведіть ,що функція f(x)=8/2-x зростає на проміжку (2;+нескінченність)
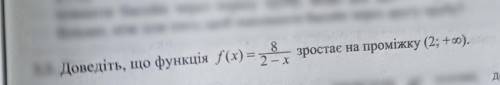
Другие вопросы по теме Алгебра
Популярные вопросы
- В одній коробці 16 кубиків, а в другій - на 4 біл ше. Скільки кубиків у другій...
3 - Два точечных заряда О1 = 1мк Кл и О2 = - 4мк Кл расположены на расстоянии...
1 - Материальная точка массой т движется по оси Ох под действием силы, направленной...
1 - As you proceed with your history, you obtain the following information. “I...
1 - Как получить белый цвет при смешивании красок?...
3 - составьте план по сказке Хуснобад....
1 - с 19 тестом , Complete the words by spelling the sound [ ǝ ] . _greem_nt_fraid...
2 - Надеюсь на скорое решение с ответом! буду очень благодарна!)...
2 - В треугольнике ABC сторона AB=12, а сторона AC=7. Найдите косинус угла A,...
3 - Визначити кількість електронів в атомі, в якому в основному стані заповнені...
1
Объяснение:
Функція зростає на проміжку, якщо її похідна набуває додатніх значень на цьому проміжку.
Знайдемо похідну функції:
Оскільки знаменник >0 завжди, то похідна набуває додатніх значень на проміжку (2;+нескінченність).
ОДЗ: х≠2
Графіком функції є гіпербола,одна з точок якої 2.
А під ту функцію просто підставте різні числа замість Х і знайдіть у. Позначте зі точки на малюнку,намалюйте гіперболу і все по ідеї.